Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
- Assessment Limits :
Long-run frequency should be greater than or equal to 300.
- Calculator :
Neutral
- Context :
Required
- Test Item #: Sample Item 1
- Question:
A spinner is divided into equal parts 1-5. George spun the spinner 300 times. A table of outcomes is shown.
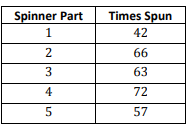
Based on the table, what is an estimated probability of the spinner landing on an even number?
- Difficulty: N/A
- Type: EE: Equation Editor
- Test Item #: Sample Item 2
- Question:
A spinner is divided into blue, green, and red parts. George spins the spinner 300 times. A table of outcomes is shown.
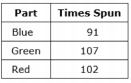
Based on this data, what is the estimated probability of the spinner landing on red?
- Difficulty: N/A
- Type: EE: Equation Editor
Related Courses
Related Access Points
Related Resources
Formative Assessments
Image/Photograph
Lesson Plans
Original Student Tutorial
Perspectives Video: Experts
Problem-Solving Tasks
Text Resource
Tutorials
Virtual Manipulatives
MFAS Formative Assessments
Students are asked to estimate the frequency of an event given its probability and explain why an expected frequency might differ from an observed frequency.
Students are asked to estimate the probability of a chance event based on observed frequencies.
Students are asked to estimate the frequency of an event given its probability and explain why an expected frequency might differ from an observed frequency.
Original Student Tutorials Mathematics - Grades 6-8
Learn how to use probability to predict expected outcomes at the Carnival in this interactive tutorial.
Student Resources
Original Student Tutorial
Learn how to use probability to predict expected outcomes at the Carnival in this interactive tutorial.
Type: Original Student Tutorial
Problem-Solving Tasks
The purpose of this task is to provide students with the opportunity to determine experimental probabilities by collecting data. The cylindrical objects used in this task typically have three different resting positions but not all of these may be equally likely and some may be extremely unlikely or impossible when the object is tossed. Furthermore, obtaining the probabilities of the outcomes is perhaps only possible through the use of long-run relative frequencies. This is because these cylinders do not have the same types of symmetries as objects that are often used as dice, such as cubes or tetrahedrons, where each outcome is equally likely.
Type: Problem-Solving Task
This task is intended as a classroom activity. Students pool the results of many repetitions of the random phenomenon (rolling dice) and compare their results to the theoretical expectation they develop by considering all possible outcomes of rolling two dice. This gives them a concrete example of what we mean by long term relative frequency.
Type: Problem-Solving Task
Tutorials
Watch the video as it predicts the number of times a spinner will land on a given outcome.
Type: Tutorial
This video demonstrates development and use of a probability model.
Type: Tutorial
Virtual Manipulatives
In this activity, students adjust how many sections there are on a fair spinner then run simulated trials on that spinner as a way to develop concepts of probability. A table next to the spinner displays the theoretical probability for each color section of the spinner and records the experimental probability from the spinning trials. This activity allows students to explore the topics of experimental and theoretical probability by seeing them displayed side by side for the spinner they have created. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.
Type: Virtual Manipulative
This online manipulative allows the student to simulate placing marbles into a bag and finding the probability of pulling out certain combinations of marbles. This allows exploration of probabilities of multiple events as well as probability with and without replacement. The tabs above the applet provide access to supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the Java applet.
Type: Virtual Manipulative
The students will play a classic game from a popular show. Through this they can explore the probability that the ball will land on each of the numbers and discover that more accurate results coming from repeated testing. The simulation can be adjusted to influence fairness and randomness of the results.
Type: Virtual Manipulative
This virtual manipulative allows one to make a random drawing box, putting up to 21 tickets with the numbers 0-11 on them. After selecting which tickets to put in the box, the applet will choose tickets at random. There is also an option which will show the theoretical probability for each ticket.
Type: Virtual Manipulative
Parent Resources
Problem-Solving Tasks
The purpose of this task is to provide students with the opportunity to determine experimental probabilities by collecting data. The cylindrical objects used in this task typically have three different resting positions but not all of these may be equally likely and some may be extremely unlikely or impossible when the object is tossed. Furthermore, obtaining the probabilities of the outcomes is perhaps only possible through the use of long-run relative frequencies. This is because these cylinders do not have the same types of symmetries as objects that are often used as dice, such as cubes or tetrahedrons, where each outcome is equally likely.
Type: Problem-Solving Task
This task is intended as a classroom activity. Students pool the results of many repetitions of the random phenomenon (rolling dice) and compare their results to the theoretical expectation they develop by considering all possible outcomes of rolling two dice. This gives them a concrete example of what we mean by long term relative frequency.
Type: Problem-Solving Task








