Clarifications
Clarification 1: Depending on the context, the solution of a division problem with a remainder may be the whole number part of the quotient, the whole number part of the quotient with the remainder, the whole number part of the quotient plus 1, or the remainder.Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Dividend
- Divisor
- Equation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
- MA.6.NSO.2.3
Purpose and Instructional Strategies
The purpose of this benchmark is for students to solve multistep word problems with whole numbers and whole-number answers involving any combination of the four operations. Work in this benchmark continues instruction from grade 4 where students interpreted remainders in division situations (MA.4.AR.1.1) (MTR.7.1), and prepares for solving multi-step word problems involving fractions and decimals in grade 6 (MA.6.NSO.2.3).- To allow for an effective transition into algebraic concepts in grade 6 (MA.6.AR.1.1), it is important for students to have opportunities to connect mathematical statements and number sentences or equations.
- During instruction, teachers should allow students an opportunity to practice with word problems that require multiplication or division which can be solved by using drawings and equations, especially as the students are making sense of the context within the problem (MTR.5.1).
- Teachers should have students practice with representing an unknown number in a word problem with a variable by scaffolding from the use of only an unknown box.
- Offer word problems to students with the numbers covered up or replaced with symbols or icons and ensure to ask students to write the equation or the number sentence to show the problem type situation (MTR.6.1).
- Interpreting number pairs on a coordinate graph can provide students opportunities to solve multi-step real-world problems with the four operations (MA.5.GR.4.2).
Common Misconceptions or Errors
- Students may apply a procedure that results in remainders that are expressed as r for ALL situations, even for those in which the result does not make sense.
- For example, when a student is asked to solve the following problem: “There are 34 students in a class bowling tournament. They plan to have 3 students in each bowling lane. How many bowling lanes will they need so that everyone can participate?” the student response is “11 r 1 bowling lanes,” without any further understanding of how many bowling lanes are needed and how the students may be divided among the last 1 or 2 lanes. To assist students with this misconception, pose the question “What does the quotient mean?”
Strategies to Support Tiered Instruction
- Instruction includes opportunities to engage in guided practice completing multi-step word problems with any combination of the four operations, including problems with remainders. Students use drawings and models to understand how to interpret the remainder in situations in which they will need to drop the remainder as their solution.
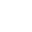
- For example, the teacher displays and reads the following problem aloud: “There are 58 fourth grade students and 45 fifth grade students going on a class field trip. They plan to have 20 students in each van. How many vans will they need so that everyone can participate?” Students use models or drawings to represent the problem and write an equation to represent the problem. The teacher uses guided questioning to encourage students to identify that they will need to add one to the quotient as their solution. If students state that they will need 5r3 vans, the teacher refers to the models to prompt students that a sixth van is needed for the remaining three students. If students state that they will need 3 more vans since the remainder is 3, the teacher reminds students through guided questioning that the remainder of 3 represents 3 remaining students and only 1 more van is needed (i.e., “add 1 to the quotient”). This is repeated with similar multistep real-world problems, asking students to explain what the quotient means in problems involving remainders.
- Instruction includes opportunities to engage in practice with explicit instruction completing multi-step word problems with any combination of the four operations, including problems with remainders. Students use manipulatives to understand how to interpret the remainder in situations in which they will need to drop the remainder as their solution.
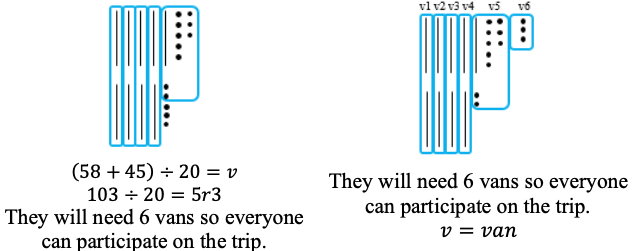
- For example, the teacher displays and reads the following problem aloud: “There are 18 red markers and 26 black markers on the art table. Ms. Williams is cleaning up and can put 10 markers in each box. How many boxes will she need so all the markers will be put into box?” The teacher uses manipulatives (e.g., base ten blocks) to represent the problem, having students write an equation to represent the problem. The teacher uses guided questioning to encourage students to identify that they will need to add 1 to the quotient as their solution. If students state that she will need 4r4 boxes, the teacher refers to the models to prompt students that a fifth box is needed for the remaining four markers. If students state that they will need 4 more boxes since the remainder is 4, the teacher reminds students through guided questioning that the remainder of 4 represents 4 remaining markers and only 1 more box is needed (i.e., “add 1 to the quotient”). This is repeated with similar multistep real-world problems, asking students to explain what the quotient means in problems involving remainders.
Instructional Tasks
Instructional Task 1 (MTR.6.1)
There are 128 girls in the Girl Scouts Troop 1653 and 154 girls in the Girl Scouts Troop 1764. Both Troops are going on a camping trip. Each bus can hold 36 girls. How many buses are needed to get all the girls to the camping site?
Instructional Items
Instructional Item 1
A shoe store orders 17 cases each containing 142 pairs of sneakers and 12 cases each containing 89 pairs of sandals. How many more pairs of sneakers did the store order?*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
Related Access Points
Related Resources
Formative Assessment
Lesson Plans
Perspectives Video: Teaching Idea
Problem-Solving Tasks
STEM Lessons - Model Eliciting Activity
In this Model Eliciting Activity, MEA, students will develop a procedure for choosing a balloon company for a birthday party and rank them from best to worst.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx
In this MEA, the students will help a charitable organization select 5 snack items from a list to provide nutritious snacks for children in low-income communities. Students will practice using the four operations to solve real-world problems and use decimal notation to make calculations involving money. Additionally, they will be asked to compare multi-digit numbers to the thousandths.
In this MEA, students will interpret data related to digital cameras to make a recommendation for a school to purchase for students to use.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx
In this MEA, students will create a procedure to rank five mini-refrigerators to determine which one should be purchased for the school by the PTA based on size, type, features, energy usage, and cost. In the process, students will solve real-world problems involving the multiplication of multi-digit numbers with decimals to the hundredths, including using money. Students will also determine the volume of a rectangular prism using a formula.
In this MEA, students evaluate the contributions of various explorers to help a museum select the subject who provided the most impact on Western development for a new exhibit. Students will need to convert units to have the necessary information to help come up with a solution to the problem.
In this Model Eliciting Activity, MEA, students will work in collaborative groups to solve multistep problems with whole numbers using the 4 operations. The students will be asked to assist a property owner, who is planning to repair his new property, in purchasing the right exterior paint. They will need to read a data table, rank the paints from highest to lowest, calculate the amount of gallons needed according to the surface area, and calculate the total cost of each paint. A twist is added to the problem when one of the paints is not available, but two others are added, and also the owner wants to paint the rectangular area of the dividing walls outside.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx
In this Model Eliciting Activity, MEA, students will work in collaborative groups to solve multistep problems with whole numbers and decimals by using different mathematical operations such as addition, subtraction, multiplication, and division. The students will be asked to assist a businessman who is planning a party for his employees. They will need to read several ads and decide which company offers the best deal in renting tables, chairs, and tablecloths for the client. They will need to take into consideration the number of guests attending the party and the budget allowed. A twist is added to the problem when the students are asked to consider an additional ad and the fact that the guest list is now slightly larger.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx
In this Model Eliciting Activity, MEA, students multiply and compare information to provide the most appropriate textbook for a county.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx
MFAS Formative Assessments
Student Resources
Problem-Solving Tasks
The purpose of this task is for students to solve multi-step problems in a context involving a concept that supports financial literacy, namely inflation. Inflation is a sustained increase in the average price level. In this task, students can see that if the price level increases and people’s incomes do not increase, they aren’t able to purchase as many goods and services; in other words, their purchasing power decreases.
Type: Problem-Solving Task
When a division problem involving whole numbers does not result in a whole number quotient, it is important for students to be able to decide whether the context requires the result to be reported as a whole number with remainder (as with Part (b)) or a mixed number/decimal (as with Part (c)). Part (a) presents two variations on a context that require these two different responses to highlight the distinction between them.
Type: Problem-Solving Task
The purpose of this task is to help students gain a better understanding of fractions and the conversion of fractions into smaller units.
Type: Problem-Solving Task
Parent Resources
Problem-Solving Tasks
The purpose of this task is for students to solve multi-step problems in a context involving a concept that supports financial literacy, namely inflation. Inflation is a sustained increase in the average price level. In this task, students can see that if the price level increases and people’s incomes do not increase, they aren’t able to purchase as many goods and services; in other words, their purchasing power decreases.
Type: Problem-Solving Task
When a division problem involving whole numbers does not result in a whole number quotient, it is important for students to be able to decide whether the context requires the result to be reported as a whole number with remainder (as with Part (b)) or a mixed number/decimal (as with Part (c)). Part (a) presents two variations on a context that require these two different responses to highlight the distinction between them.
Type: Problem-Solving Task
The purpose of this task is to help students gain a better understanding of fractions and the conversion of fractions into smaller units.
Type: Problem-Solving Task