Related Benchmarks
Related Access Points
Access Points
Related Resources
Educational Game
Formative Assessments
Image/Photograph
Lesson Plans
Original Student Tutorials
Perspectives Video: Expert
Perspectives Video: Teaching Ideas
Problem-Solving Tasks
Tutorials
Virtual Manipulative
Student Resources
Original Student Tutorials
Learn about equivalent 10ths and 100ths and how to calculate these equivalent fractions at the fair in this interactive tutorial.
Type: Original Student Tutorial
Find the total amounts of repeated fraction quantities by multiplying a fraction by a whole number using visual models that represent real-world problems and cookies in this interactive tutorial.
Type: Original Student Tutorial
Learn how to decompose a fraction into a sum of fractions with common denominators with this interactive tutorial.
Type: Original Student Tutorial
Educational Game
This fun and interactive game helps practice estimation skills, using various operations of choice, including addition, subtraction, multiplication, division, using decimals, fractions, and percents.
Various levels of difficulty make this game appropriate for multiple age and ability levels.
Addition/Subtraction: The addition and subtraction of whole numbers, the addition and subtraction of decimals.
Multiplication/Division: The multiplication and addition of whole numbers.
Percentages: Identify the percentage of a whole number.
Fractions: Multiply and divide a whole number by a fraction, as well as apply properties of operations.
Type: Educational Game
Problem-Solving Tasks
The purpose of this task is adding fractions with a focus on tenths and hundredths.
Type: Problem-Solving Task
This task is a straightforward task related to adding fractions with the same denominator. The main purpose is to emphasize that there are many ways to decompose a fraction as a sum of fractions.
Type: Problem-Solving Task
The purpose of this task is for students to show they understand the connection between fraction and decimal notation by writing the same numbers both ways. Comparing and contrasting the two solutions shown below shows why decimal notation can be confusing. The first solution shows the briefest way to represent each number, and the second solution makes all the zeros explicit.
Type: Problem-Solving Task
The purpose of this task is to help students understand and articulate the reasons for the steps in the usual algorithm for converting a mixed number into an equivalent fraction. Step two shows that the algorithm is merely a shortcut for finding a common denominator between two fractions. This concept is an important precursor to adding mixed numbers and fractions with like denominators and as such, step two should be a point of emphasis. This task is appropriate for either instruction or formative assessment.
Type: Problem-Solving Task
This task provides a familiar context allowing students to visualize multiplication of a fraction by a whole number. This task could form part of a very rich activity which includes studying soda can labels.
Type: Problem-Solving Task
This task provides a context where it is appropriate for students to subtract fractions with a common denominator; it could be used for either assessment or instructional purposes. For this particular task, teachers should anticipate two types of solution approaches: one where students subtract the whole numbers and the fractions separately and one where students convert the mixed numbers to improper fractions and then proceed to subtract.
Type: Problem-Solving Task
The purpose of this task is to have students think about the meaning of multiplying a number by a fraction, and use this burgeoning understanding of fraction multiplication to make sense of the commutative property of multiplication in the case of fractions.
Type: Problem-Solving Task
The purpose of this task is to have students add mixed numbers with like denominators. This task illustrates the different kinds of solution approaches students might take to such a task. Two general approaches should be anticipated: one where students calculate exactly how many buckets of blocks the boys have to determine an answer, and one where students compare the given numbers to benchmark numbers.
Type: Problem-Solving Task
Tutorials
The Khan Academy tutorial video presents a visual fraction model for adding 3/10 + 7/100 .
Type: Tutorial
In this Khan Academy video visual fraction models are used to represent the multiplication of a whole number times a fraction.
Type: Tutorial
This Khan Academy video uses authentic pictures to present addition of two fractions with common denominators.
Type: Tutorial
This Khan Academy video solves two word problems using visual fraction models.
Type: Tutorial
Virtual Manipulative
This virtual manipulative allows individual students to work with fraction relationships. (There is also a link to a two-player version.)
Type: Virtual Manipulative
Parent Resources
Image/Photograph
Illustrations that can be used for teaching and demonstrating fractions. Fractional representations are modeled in wedges of circles ("pieces of pie") and parts of polygons. There are also clipart images of numerical fractions, both proper and improper, from halves to twelfths. Fraction charts and fraction strips found in this collection can be used as manipulatives and are ready to print for classroom use.
Type: Image/Photograph
Problem-Solving Tasks
The purpose of this task is adding fractions with a focus on tenths and hundredths.
Type: Problem-Solving Task
This task is a straightforward task related to adding fractions with the same denominator. The main purpose is to emphasize that there are many ways to decompose a fraction as a sum of fractions.
Type: Problem-Solving Task
The purpose of this task is for students to show they understand the connection between fraction and decimal notation by writing the same numbers both ways. Comparing and contrasting the two solutions shown below shows why decimal notation can be confusing. The first solution shows the briefest way to represent each number, and the second solution makes all the zeros explicit.
Type: Problem-Solving Task
The purpose of this task is to help students understand and articulate the reasons for the steps in the usual algorithm for converting a mixed number into an equivalent fraction. Step two shows that the algorithm is merely a shortcut for finding a common denominator between two fractions. This concept is an important precursor to adding mixed numbers and fractions with like denominators and as such, step two should be a point of emphasis. This task is appropriate for either instruction or formative assessment.
Type: Problem-Solving Task
This task provides a familiar context allowing students to visualize multiplication of a fraction by a whole number. This task could form part of a very rich activity which includes studying soda can labels.
Type: Problem-Solving Task
This task provides a context where it is appropriate for students to subtract fractions with a common denominator; it could be used for either assessment or instructional purposes. For this particular task, teachers should anticipate two types of solution approaches: one where students subtract the whole numbers and the fractions separately and one where students convert the mixed numbers to improper fractions and then proceed to subtract.
Type: Problem-Solving Task
The purpose of this task is to have students think about the meaning of multiplying a number by a fraction, and use this burgeoning understanding of fraction multiplication to make sense of the commutative property of multiplication in the case of fractions.
Type: Problem-Solving Task
The purpose of this task is to have students add mixed numbers with like denominators. This task illustrates the different kinds of solution approaches students might take to such a task. Two general approaches should be anticipated: one where students calculate exactly how many buckets of blocks the boys have to determine an answer, and one where students compare the given numbers to benchmark numbers.
Type: Problem-Solving Task






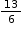 and record their work with an equation.
and record their work with an equation.
