Given the graph or table of values of two or more transformations of a function, state the type of transformation and find the values of the real number that defines the transformation.
General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Functions
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
- MA.912.AR.2.4
- MA.912.AR.2.5
- MA.912.AR.3.7
- MA.912.AR.3.8
- MA.912.AR.4.4
- MA.912.AR.5.6
- MA.912.AR.5.7
- MA.912.AR.5.8
- MA.912.AR.5.9
- MA.912.F.1.1
Terms from the K-12 Glossary
- Transformation
- Translation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students performed single transformations on two-dimensional figures. In Algebra I, students identified the effects of single transformations on linear, quadratic and absolute value functions. In Geometry, students performed multiple transformations on two-dimensional figures. In Mathematics for College Algebra, students determine the type of transformations on linear, quadratic, exponential, logarithmic and absolute value functions.- Instruction includes identifying function transformations involving a combination of translations, dilations and reflections, and determining the value of the real number that defines each of the transformations.
- Transformations can be either horizontal (changes to the input: ) or vertical (changes to the output: ()).
- There are three different types of transformations: translations, dilations and reflections.
- By combining single transformations, a parent function can become a more advanced function.

- Using a graphing utility can help students understand how changing the value of the real numbers in the function’s equation change its graph (MTR.5.1).
- Encourage student’s discussion about the effects of changing the value of the real numbers , , and in the equation of the function (MTR.4.1). Ask them to generalize their findings.
- Instruction includes determining the order for performing two or more transformations to a single function. A different order of transformations may result in a different outcome.
- It is helpful to relate the order of the transformations to the order of operations.
- Horizontal shifts
- Vertical stretching or shrinking
- Reflecting
- Vertical shift
- It is helpful to relate the order of the transformations to the order of operations.
Common Misconceptions or Errors
- Some students may have difficulty seeing the impact of a transformation when comparing tables and graphs. In these cases, encourage students to convert the graph to a second table, using the same domain as the first table. This should aid in comparisons (MTR.2.1).
- Similar to writing functions in vertex form, students may confuse the effect of the sign of in ( + ). Direct these students to examine a graph of the two functions to see that the horizontal shift is opposite of the sign of .
- Vertical stretch/compression can be hard for students to see on linear functions initially and they may interpret stretch/compression as rotation. Introduce the effects of () and () by using a quadratic or absolute value function first before analyzing the effect on a linear function.
- Students may think that a vertical and horizontal stretch from () and () look the same. For linear and quadratic functions, it can help to have a non-zero -intercept to visualize the difference.
Instructional Tasks
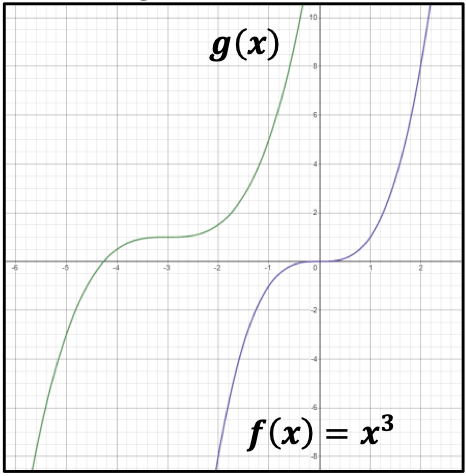
Instructional Task 1 (MTR.3.1)- Below are the graphs of () and ().
- Part A. Describe the sequence of transformations that map the graph of () to the graph of ().
- Part B. If () = , write an equation for ().
Instructional Task 2 (MTR.3.1, MTR.5.1)
- The tables below show a sequence of transformation for function .
- Part A. Describe the transformation of () represented in Step 1. State the value of .
- Part B. Describe the transformation of () represented in Step 2. State the value of .
- Part C. Describe the transformation of () represented in Step 3. State the value of .
- Part D. Write an equation for () in terms of ().
Instructional Items
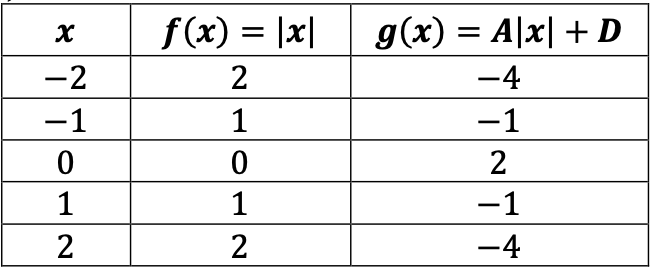
Instructional Item 1- Given the table below, determine the value of and .
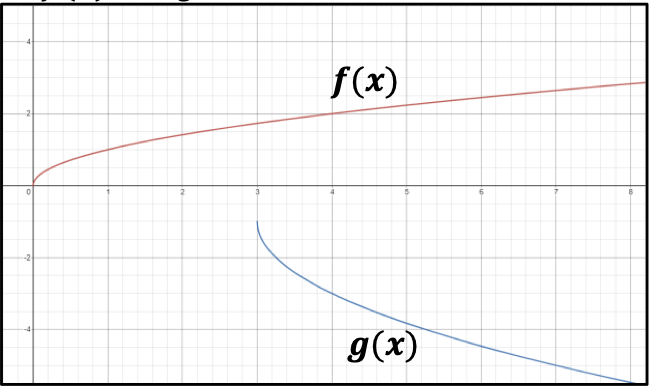
- In the graph below, function is obtained from function through a sequence of transformations. Find an equation for .
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
This benchmark is part of these courses.
1200710: Mathematics for College Algebra (Specifically in versions: 2022 - 2024, 2024 and beyond (current))
Related Access Points
Alternate version of this benchmark for students with significant cognitive disabilities.
Related Resources
Vetted resources educators can use to teach the concepts and skills in this benchmark.
Lesson Plans
Student Resources
Vetted resources students can use to learn the concepts and skills in this benchmark.
Parent Resources
Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.







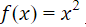 .
.
