General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
- MA.912.AR.2.4
- MA.912.AR.2.5
- MA.912.AR.3.7
- MA.912.AR.3.8
- MA.912.AR.4.4
- MA.912.AR.5.6
- MA.912.AR.5.7
- MA.912.AR.5.8
- MA.912.AR.5.9
- MA.912.F.1.1
Terms from the K-12 Glossary
- Transformation
- Translation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students performed single transformations on two-dimensional figures. In Algebra I, students identified the effects of single transformations on linear, quadratic and absolute value functions. In Geometry, students performed multiple transformations on two-dimensional figures. In Mathematics for College Algebra, students determine the type of transformations on linear, quadratic, exponential, logarithmic and absolute value functions.- Instruction includes identifying function transformations involving a combination of translations, dilations and reflections, and determining the value of the real number that defines each of the transformations.
- Transformations can be either horizontal (changes to the input: ) or vertical (changes to the output: ()).
- There are three different types of transformations: translations, dilations and reflections.
- By combining single transformations, a parent function can become a more advanced function.

- Using a graphing utility can help students understand how changing the value of the real numbers in the function’s equation change its graph (MTR.5.1).
- Encourage student’s discussion about the effects of changing the value of the real numbers , , and in the equation of the function (MTR.4.1). Ask them to generalize their findings.
- Instruction includes determining the order for performing two or more transformations to a single function. A different order of transformations may result in a different outcome.
- It is helpful to relate the order of the transformations to the order of operations.
- Horizontal shifts
- Vertical stretching or shrinking
- Reflecting
- Vertical shift
- It is helpful to relate the order of the transformations to the order of operations.
Common Misconceptions or Errors
- Some students may have difficulty seeing the impact of a transformation when comparing tables and graphs. In these cases, encourage students to convert the graph to a second table, using the same domain as the first table. This should aid in comparisons (MTR.2.1).
- Similar to writing functions in vertex form, students may confuse the effect of the sign of in ( + ). Direct these students to examine a graph of the two functions to see that the horizontal shift is opposite of the sign of .
- Vertical stretch/compression can be hard for students to see on linear functions initially and they may interpret stretch/compression as rotation. Introduce the effects of () and () by using a quadratic or absolute value function first before analyzing the effect on a linear function.
- Students may think that a vertical and horizontal stretch from () and () look the same. For linear and quadratic functions, it can help to have a non-zero -intercept to visualize the difference.
Instructional Tasks
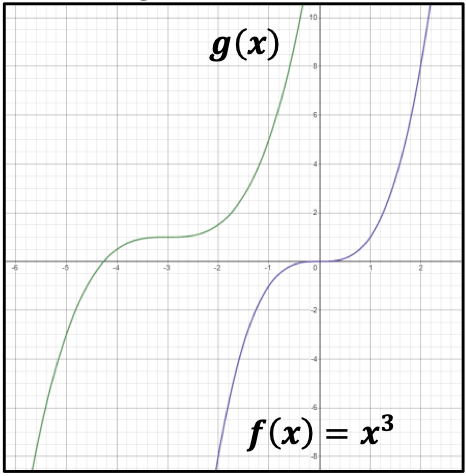
Instructional Task 1 (MTR.3.1)- Below are the graphs of () and ().
- Part A. Describe the sequence of transformations that map the graph of () to the graph of ().
- Part B. If () = , write an equation for ().
Instructional Task 2 (MTR.3.1, MTR.5.1)
- The tables below show a sequence of transformation for function .
- Part A. Describe the transformation of () represented in Step 1. State the value of .
- Part B. Describe the transformation of () represented in Step 2. State the value of .
- Part C. Describe the transformation of () represented in Step 3. State the value of .
- Part D. Write an equation for () in terms of ().
Instructional Items
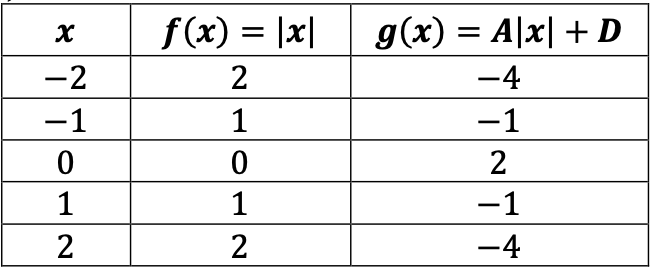
Instructional Item 1- Given the table below, determine the value of and .
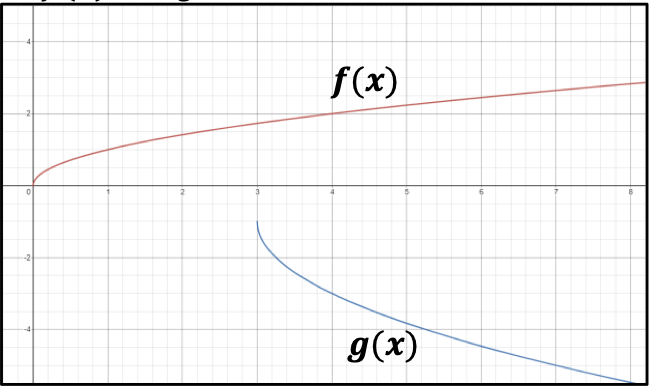
- In the graph below, function is obtained from function through a sequence of transformations. Find an equation for .
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.


 .
.