Clarifications
Clarification 1: Instruction focuses on the relationship between the area of a rectangle and the area of a right triangle.Clarification 2: Within this benchmark, the expectation is to know from memory a formula for the area of a triangle.
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Algorithm
- Area
- Rectangle
- Triangle
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
Students will use their understanding from grade 5 of models and formulas to find the area of a rectangle to derive the formula to find the area of a triangle (MTR.1.1, MTR.2.1). Students will extend this knowledge in grade 7 to decompose composite figures into triangles and quadrilaterals in order to find area.- Instruction includes developing the understanding that two copies of any right triangle will always form a rectangle with the same base and height. Therefore, the triangle has an area of half of the rectangle, = ( × ). This understanding can develop from seeing how a triangle is constructed when cutting a rectangular piece of paper diagonally in half.
- Students should be flexible in their understanding of formulas to be able to use show the equivalency of and .
- Formulas can be a tool or strategy for geometric reasoning. Students require a solid understanding of two area concepts: (1) the area of a rectangle is × or × , and (2) figures of the same size and shape (congruent) have the same area.
- Instruction includes representing measurements for area as square units, units squared or units2.
- Students should understand that any side of the triangle can be a base; however, the height can only be represented as a line segment drawn from a vertex perpendicular to the base. The terms height and altitude can be used interchangeably. Students should see the right-angle symbol,
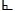 to indicate perpendicularity.
to indicate perpendicularity. - Problem types include having students’ measure lengths using a ruler to determine the area.
Common Misconceptions or Errors
- Students may forget that multiplying by and dividing by are the same operation.
- Students may neglect to apply the when finding the area of a triangle.
- Students may incorrectly identify a side measurement as the height of a triangle.
Strategies to Support Tiered Instruction
- Teacher models several problems solving them both ways (using a rectangle and using a formula) and then have the students solve them step by step guiding them to the answer. This will provide students with the opportunity to see that the two operations are identical.
- Teacher reinforces that a right triangle is half of a rectangle, therefore we must cut the area in half.
- Teacher models with geometric software so students can see that a right triangle is half of a rectangle, which is why we multiply by .
- Teacher models the use of manipulatives that students can measure to better understand there is a difference between a side length and the height in non-right triangles.
Instructional Tasks
Instructional Task 1 (MTR.2.1, MTR.4.1)Mrs. Lito asked her students to label a base and its corresponding height in the triangle shown.
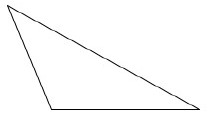
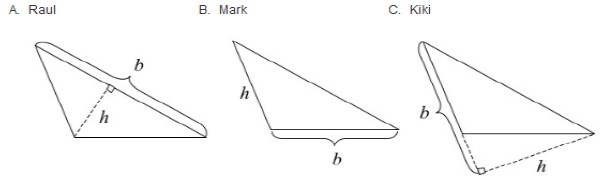
- Part A. Which students, if any, have correctly identified a base and its corresponding height? Which ones have not? Explain what is incorrect.
- Part B. There are three possible base-height pairs for this triangle. Sketch all three.
Instructional Task 2 (MTR.5.1)
Look at the triangles below.
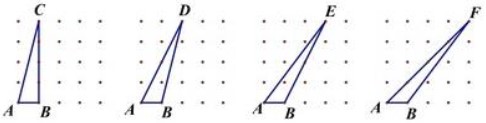
- Which triangle has the greatest area?
- Which triangle has the least area?
- Do any of the triangles have the same area?
- Are some areas impossible to compare?
Instructional Items
Instructional Item 1Find the area of Δ.
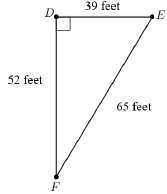
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
Related Access Points
Related Resources
Formative Assessment
Image/Photograph
Lesson Plans
Original Student Tutorial
Problem-Solving Tasks
Tutorial
MFAS Formative Assessments
Original Student Tutorials Mathematics - Grades 6-8
Follow George as he explores the formula for the area of a triangle and uses it to find the area of various triangles in this interactive student tutorial.
Student Resources
Original Student Tutorial
Follow George as he explores the formula for the area of a triangle and uses it to find the area of various triangles in this interactive student tutorial.
Type: Original Student Tutorial
Problem-Solving Task
Students are asked to determine and illustrate all possible descriptions for the base and height of a given triangle.
Type: Problem-Solving Task
Tutorial
We will be able to find the area of a triangle in a coordinate grid. The formula for the area of a triangle is given in this tutorial.
Type: Tutorial
Parent Resources
Image/Photograph
In this lesson, you will find clip art and various illustrations of polygons, circles, ellipses, star polygons, and inscribed shapes.
Type: Image/Photograph
Problem-Solving Task
Students are asked to determine and illustrate all possible descriptions for the base and height of a given triangle.
Type: Problem-Solving Task









