Standard #: MA.6.GR.2.1

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.6.NSO.2.1
• MA.6.AR.2.3

 

Terms from the K-12 Glossary

• Algorithm
• Area
• Rectangle
• Triangle

 

Vertical Alignment

Previous Benchmarks

• MA.5.GR.2.1

Next Benchmarks

• MA.7.GR.1.2

 

Purpose and Instructional Strategies

Students will use their understanding from grade 5 of models and formulas to find the area of a rectangle to derive the formula to find the area of a triangle (MTR.1.1, MTR.2.1). Students will extend this knowledge in grade 7 to decompose composite figures into triangles and quadrilaterals in order to find area. 

• Instruction includes developing the understanding that two copies of any right triangle will always form a rectangle with the same base and height. Therefore, the triangle has an area of half of the rectangle, $A$ = $\frac{\text{1}}{\text{2}}$ ($b$$a$$s$$e$ × $h$$e$$i$$g$$h$$t$). This understanding can develop from seeing how a triangle is constructed when cutting a rectangular piece of paper diagonally in half.
• Students should be flexible in their understanding of formulas to be able to use show the equivalency of $\frac{\text{1}}{\text{2}}$$b$$h$ and $\frac{\text{<i>bh</i>}}{\text{2}}$.
• Formulas can be a tool or strategy for geometric reasoning. Students require a solid understanding of two area concepts: (1) the area of a rectangle is $l$$e$$n$$g$$t$$h$ × $w$$i$$d$$t$$h$ or $b$$a$$s$$e$ × $h$$e$$i$$g$$h$$t$, and (2) figures of the same size and shape (congruent) have the same area.
• Instruction includes representing measurements for area as square units, units squared or units².
• Students should understand that any side of the triangle can be a base; however, the height can only be represented as a line segment drawn from a vertex perpendicular to the base. The terms height and altitude can be used interchangeably. Students should see the right-angle symbol, 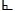 to indicate perpendicularity.
• Problem types include having students’ measure lengths using a ruler to determine the area.

 

Common Misconceptions or Errors

• Students may forget that multiplying by and dividing by $\frac{\text{1}}{\text{2}}$ are the same operation.
• Students may neglect to apply the $\frac{\text{1}}{\text{2}}$ when finding the area of a triangle.
• Students may incorrectly identify a side measurement as the height of a triangle.

 

Strategies to Support Tiered Instruction

• Teacher models several problems solving them both ways (using a rectangle and using a formula) and then have the students solve them step by step guiding them to the answer. This will provide students with the opportunity to see that the two operations are identical.
• Teacher reinforces that a right triangle is half of a rectangle, therefore we must cut the area in half.
• Teacher models with geometric software so students can see that a right triangle is half of a rectangle, which is why we multiply by $\frac{\text{1}}{\text{2}}$.
• Teacher models the use of manipulatives that students can measure to better understand there is a difference between a side length and the height in non-right triangles.

 

Instructional Tasks

Instructional Task 1 (MTR.2.1, MTR.4.1)
Mrs. Lito asked her students to label a base $b$ and its corresponding height $h$ in the triangle shown.Three students drew the figures below.

 

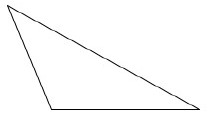
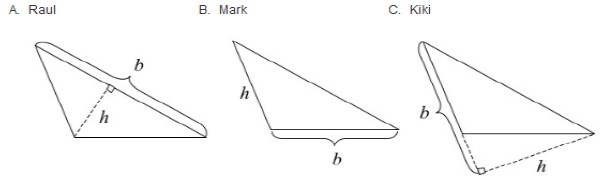
• Part A. Which students, if any, have correctly identified a base and its corresponding height? Which ones have not? Explain what is incorrect.
• Part B. There are three possible base-height pairs for this triangle. Sketch all three.

Instructional Task 2 (MTR.5.1)
Look at the triangles below.Determine and explain:

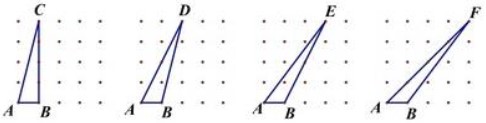
• Which triangle has the greatest area?
• Which triangle has the least area?
• Do any of the triangles have the same area?
• Are some areas impossible to compare?

 

Instructional Items

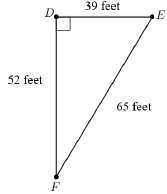
Instructional Item 1
Find the area of Δ$D$$E$$F$.

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.