Remarks
Example 1: A zoo has turtles (each with four legs) and pelicans (each with two legs). There were 29 animals and 78 legs. How many of each type of animal were there? Your final solution should involve principles of equality.
Example 2: The students in Mr. Kemp's class ordered T-shirts for the class. They found two different quotes for the cost of the shirts.
Company A charges $4 per shirt.
Company B charges $75 plus $3 per shirt.
1. The class plans to order 30 shirts. Which company will be a better deal?
2. For what number of T-shirts is the cost the same for both companies?
3. Does the company you chose for question 1 always offer a better deal? Why or why not? Explain your answers.
Students should be encouraged to make tables, graphs, and equations and notice the interconnectedness of these representations.
-
Item Type(s):
This benchmark may be assessed using:
MC
,
GR
item(s)
Also assesses MA.8.A.1.4 Identify the solution to a system of linear equations using graphs.
- Clarification :
Students will solve problems that can be represented by a system of two linear equations.
Students will identify the unique solution for a system of equations representing two intersecting lines.
Students will understand that a specific system of equations representing parallel lines has no solution.
- Content Limits :
Graphs used in items may include all four quadrants.
Items should rely primarily on tables, graphs, or models to present problems.
Items may assess knowledge of the slopes of lines (including vertical and horizontal lines) and the x- and y-intercepts of lines.
Items may assess properties of parallel or perpendicular lines. - Stimulus Attributes :
Context or problems should enable students to solve using concrete or pictorial representations of models, tables, and graphs, rather than solve abstractly using algebraic symbolism.
Graphics should be used for all of these items.
- Test Item #: Sample Item 1
- Question: Caleb is buying small and large containers of coffee. He purchased 5 containers of coffee that weighed a total of 40 pounds. The small containers weigh 5 pounds and the large containers weigh 10 pounds. The equations and graph below can be used to determine the number of each type of container Caleb purchased, where x represents the small container and y represents the large container.
Number of containers: x + y = 5
Total weight of coffee: 5x + 10y = 40
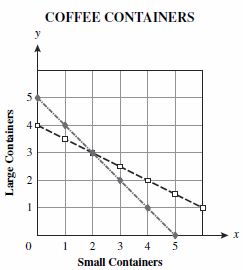
What are the number of small containers and large containers Caleb purchased? - Difficulty: N/A
- Type: MC: Multiple Choice
- Test Item #: Sample Item 2
- Question: An economist is helping a paper company evaluate the demand for reams of paper at different selling prices. The point at which the supply and demand graphs intersect is referred to as market equilibrium.
The economist graphed the supply and demand equations shown below.
Demand equation: y = -0.1x + 12
Supply equation: y = 0.11x - 2.7

What is the price per ream, in dollars, of the market equilibrium?
- Difficulty: N/A
- Type: GR: Gridded-Response
Related Access Points
Related Resources
Educational Software / Tool
Formative Assessment
Problem-Solving Task
Virtual Manipulative
Student Resources
Problem-Solving Task
In this online problem-solving challenge, students apply algebraic reasoning to determine the "costs" of individual types of faces from sums of frowns, smiles, and neutral faces. This page provides three pictorial problems involving solving systems of equations along with tips for thinking through the problem, the solution, and other similar problems.
Type: Problem-Solving Task
Virtual Manipulative
This activity allows the user to graph data sets in multiple bar graphs. The color, thickness, and scale of the graph are adjustable which may produce graphs that are misleading. Users may input their own data, or use or alter pre-made data sets. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.
Type: Virtual Manipulative
Parent Resources
Problem-Solving Task
In this online problem-solving challenge, students apply algebraic reasoning to determine the "costs" of individual types of faces from sums of frowns, smiles, and neutral faces. This page provides three pictorial problems involving solving systems of equations along with tips for thinking through the problem, the solution, and other similar problems.
Type: Problem-Solving Task







