- Recognize opposite signs of numbers as indicating locations on opposite sides of 0 on the number line; recognize that the opposite of the opposite of a number is the number itself, e.g., –(–3) = 3, and that 0 is its own opposite.
- Understand signs of numbers in ordered pairs as indicating locations in quadrants of the coordinate plane; recognize that when two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
- Find and position integers and other rational numbers on a horizontal or vertical number line diagram; find and position pairs of integers and other rational numbers on a coordinate plane.
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
-
Also Assesses:
- Assessment Limits :
Plotting of points in the coordinate plane should include some negative values (not just first quadrant). Numbers in MAFS.6.NS.3.8 must be positive or negative rational numbers. Do not use polygons/vertices for MAFS.6.NS.3.8. Do not exceed a 10 × 10 coordinate grid, though scales can vary. - Calculator :
No
- Context :
Allowable
MAFS.6.NS.3.8
- Test Item #: Sample Item 1
- Question:
What is the opposite of -5?
- Difficulty: N/A
- Type: EE: Equation Editor
- Test Item #: Sample Item 2
- Question:
What is the value of the x-coordinate that is 9 units to the left of (5,-8)?
- Difficulty: N/A
- Type: EE: Equation Editor
- Test Item #: Sample Item 3
- Question: Which ordered pair best describes the point plotted in Quadrant II on the
coordinate plane shown?
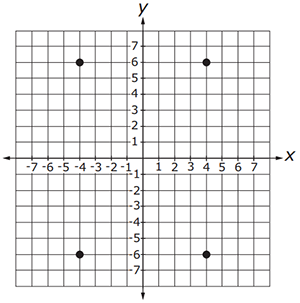
- Difficulty: N/A
- Type: MC: Multiple Choice
Related Courses
Related Access Points
Related Resources
Educational Game
Formative Assessments
Lesson Plans
Original Student Tutorials
Perspectives Video: Professional/Enthusiast
Problem-Solving Task
Student Center Activity
Tutorials
Video/Audio/Animation
MFAS Formative Assessments
Students are asked to graph -4, 0, and 4 on a number line and to explain the relationship between a number and its opposite in terms of the number line.
Students are asked to graph points given their coordinates and describe the coordinates of graphed points when the axes have different scales.
Students are asked to graph points given their coordinates and describe the coordinates of graphed points.
Students are asked to find the coordinates of graphed points and graph points with rational coordinates on a number line.
Students are asked to determine in what quadrant or on which axis, points described algebraically, are located.
Students are asked to compare the graphs of coordinates that are opposite in sign on a number line and in the coordinate plane.
Original Student Tutorials Mathematics - Grades 6-8
Explore reflections on a coordinate plane in epic Capture the Flag tournament with this interactive tutorial.
This is part 2 in a two-part series:
Learn how to create and use number lines with positive and negative numbers, graph positive and negative numbers, find their distance from zero, find a number’s opposite using a number line and signs, and recognize that zero is its own opposite with this interactive, golf-themed tutorial.
Student Resources
Original Student Tutorials
Explore reflections on a coordinate plane in epic Capture the Flag tournament with this interactive tutorial.
This is part 2 in a two-part series:
- Open "Capturing Flags on the Coordinate Plane Part 1"
- Open "Capturing Flags on the Coordinate Plane Part 2"
Type: Original Student Tutorial
Learn how to create and use number lines with positive and negative numbers, graph positive and negative numbers, find their distance from zero, find a number’s opposite using a number line and signs, and recognize that zero is its own opposite with this interactive, golf-themed tutorial.
Type: Original Student Tutorial
Educational Game
In this activity, students enter coordinates to make a path to get to a target destination while avoiding mines. This activity allows students to explore Cartesian coordinates and the Cartesian coordinate plane. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.
Type: Educational Game
Problem-Solving Task
The purpose of this task is meant to reinforce students' understanding of rational numbers as points on the number line and to provide them with a visual way of understanding that the sum of a number and its additive inverse (usually called its "opposite") is zero.
Type: Problem-Solving Task
Student Center Activity
Students can practice answering mathematics questions on a variety of topics. With an account, students can save their work and send it to their teacher when complete.
Type: Student Center Activity
Tutorials
In this tutorial, you will compare rational numbers using a number line.
Type: Tutorial
Students will plot an ordered pair on the x (horizontal) axis and y (vertical) axis of the coordinate plane.
Type: Tutorial
This video contains examples of plotting coordinate pairs and identifying their quadrant.
Type: Tutorial
This video discusses the negative sign as meaning "opposite."
Type: Tutorial
Locate fractions and decimals on the same number line in this tutorial.
Type: Tutorial
In this tutorial, you will learn how to order rational numbers using a number line.
Type: Tutorial
This video guides you through comparisons of values, including opposites.
Type: Tutorial
This video demonstrates evaluating inequality statements, some involving absolute value, using a number line.
Type: Tutorial
Students will learn how to identify the four quadrants in the coordinate plane.
Type: Tutorial
This video uses a number line to describe the opposite of a number.
Type: Tutorial
The Cartesian Coordinate system, formed from the Cartesian product of the real number line with itself, allows algebraic equations to be visualized as geometric shapes in two or three dimensions. While this tutorial includes the basis of Coordinate system, it also includes ideas beyond fifth grade standards. Most likely only advanced fifth graders would find the video engaging.
Type: Tutorial
The first fractions used by ancient civilizations were "unit fractions." Later, numerators other than one were added, creating "vulgar fractions" which became our modern fractions. Together, fractions and integers form the "rational numbers."
Type: Tutorial
Number systems evolved from the natural "counting" numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line.
Type: Tutorial
Students will be able to see examples of addition of integers while watching a short video, and practice adding integers using an online quiz.
Type: Tutorial
Parent Resources
Problem-Solving Task
The purpose of this task is meant to reinforce students' understanding of rational numbers as points on the number line and to provide them with a visual way of understanding that the sum of a number and its additive inverse (usually called its "opposite") is zero.
Type: Problem-Solving Task
Tutorial
Students will be able to see examples of addition of integers while watching a short video, and practice adding integers using an online quiz.
Type: Tutorial