- Interpret the product (a/b) × q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a × q ÷ b. For example, use a visual fraction model to show (2/3) × 4 = 8/3, and create a story context for this equation. Do the same with (2/3) × (4/5) = 8/15. (In general, (a/b) × (c/d) = ac/bd.)
- Find the area of a rectangle with fractional side lengths by tiling it with unit squares of the appropriate unit fraction side lengths, and show that the area is the same as would be found by multiplying the side lengths. Multiply fractional side lengths to find areas of rectangles, and represent fraction products as rectangular areas.
Remarks
Examples of Opportunities for In-Depth FocusWhen students meet this standard, they fully extend multiplication to fractions, making division of fractions in grade 6 (6.NS.1) a near target.
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
-
Also Assesses:
MAFS.5.NF.2.6 Solve real-world problems involving multiplication of fractions and
mixed numbers, e.g., by using visual fraction models or equations to represent
the problem.
- Assessment Limits :
Visual models may include:- Any appropriate fraction model (e.g., circles, tape diagrams, polygons, etc.)
- Rectangle models tiled with unit squares
- Calculator :
No
- Context :
Allowable for MAFS.5.NF.2.4.
Required for MAFS.5.NF.2.6
- Test Item #: Sample Item 1
- Question:
Which expression is equivalent to
 ?
? - Difficulty: N/A
- Type: MC: Multiple Choice
- Test Item #: Sample Item 2
- Question:
Roger has
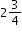 gallons of water in a jug. He pours
gallons of water in a jug. He pours 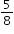 of the water into a new container.
of the water into a new container.How many gallons of water does Roger have left in the jug?
- Difficulty: N/A
- Type: EE: Equation Editor
- Test Item #: Sample Item 3
- Question:
Courtney has 4 gallons of milk. She uses
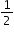 of the milk to make hot chocolate.
of the milk to make hot chocolate.She uses
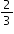 of the remaining milk to make cookies.
of the remaining milk to make cookies.How many gallons of milk does Courtney have left after making hot chocolate and cookies?
- Difficulty: N/A
- Type: EE: Equation Editor
- Test Item #: Sample Item 4
- Question: MAFS.5.NF.2.4b:
What is the area, in square units, of the rectangle?

- Difficulty: N/A
- Type: EE: Equation Editor
Related Courses
Related Access Points
Related Resources
Educational Games
Formative Assessments
Lesson Plans
Original Student Tutorials
Problem-Solving Tasks
Professional Development
Tutorials
STEM Lessons - Model Eliciting Activity
This Model Eliciting Activity (MEA) asks students to develop a procedure to select a hurricane shutter company based on several data points.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx
MFAS Formative Assessments
Students are asked to consider an equation involving multiplication of fractions, then create a visual fraction model, and write a story context to match.
Students are asked to consider an equation involving multiplication of a fraction by a whole number and create a visual fraction model. Additionally, the student is asked to interpret multiplying the number of parts by the whole number.
Students determine the area of a rectangle with given fractional dimensions by multiplying. Students are then asked to draw a model to find the area of the same rectangle.
Students interpret a visual fraction model showing multiplication of two fractions less than one.
Original Student Tutorials Mathematics - Grades K-5
Help Buffy the Baker use visual models to multiply fractions less than one as he runs his bakery in this interactive tutorial.
This is part 1 of a 4-part series. Click below to open other tutorials in the series.
Help Buffy the Baker multiply fractions less than one by relating the standard algorithm to visual models as he runs his bakery in this interactive tutorial.
This is part 2 of a 4-part series. Click below to open other tutorials in the series.
Help Buffy multiply fractions by whole numbers using the standard algorithm in addition to visual fraction models in this bakery-themed, interactive tutorial.
This is part 4 of a 4-part series. Click below to open other tutorials in the series.
Student Resources
Original Student Tutorials
Help Buffy multiply fractions by whole numbers using the standard algorithm in addition to visual fraction models in this bakery-themed, interactive tutorial.
This is part 4 of a 4-part series. Click below to open other tutorials in the series.
Type: Original Student Tutorial
Help Buffy the Baker multiply fractions less than one by relating the standard algorithm to visual models as he runs his bakery in this interactive tutorial.
This is part 2 of a 4-part series. Click below to open other tutorials in the series.
Type: Original Student Tutorial
Help Buffy the Baker use visual models to multiply fractions less than one as he runs his bakery in this interactive tutorial.
This is part 1 of a 4-part series. Click below to open other tutorials in the series.
- Part 2: Multiplying Fractions
- Part 3 Using Models to Multiply a Fraction by a Whole Number
- Part 4: Multiplying a Fraction by a Whole Number - Standard Algorithm
Type: Original Student Tutorial
Educational Games
This fun and interactive game helps practice estimation skills, using various operations of choice, including addition, subtraction, multiplication, division, using decimals, fractions, and percents.
Various levels of difficulty make this game appropriate for multiple age and ability levels.
Addition/Subtraction: The addition and subtraction of whole numbers, the addition and subtraction of decimals.
Multiplication/Division: The multiplication and addition of whole numbers.
Percentages: Identify the percentage of a whole number.
Fractions: Multiply and divide a whole number by a fraction, as well as apply properties of operations.
Type: Educational Game
Test your fraction skills by answering questions on this site. This quiz asks you to simplify fractions, convert fractions to decimals and percentages, and answer algebra questions involving fractions. You can even choose difficulty level, question types, and time limit.
Type: Educational Game
Problem-Solving Tasks
The purpose of this task is for students to find the answer to a question in context that can be represented by fraction multiplication. This task is appropriate for either instruction or assessment depending on how it is used and where students are in their understanding of fraction multiplication.
Type: Problem-Solving Task
This tasks lends itself very well to multiple solution methods. Students may learn a lot by comparing different methods. Students who are already comfortable with fraction multiplication can go straight to the numeric solutions given below. Students who are still unsure of the meanings of these operations can draw pictures or diagrams.
Type: Problem-Solving Task
The task could be one of the first activities for introducing the multiplication of fractions. The task has fractions which are easy to draw and provides a linear situation. Students benefit from reasoning through the solution to such word problems before they are told that they can be solved by multiplying the fractions; this helps them develop meaning for fraction multiplication.
Type: Problem-Solving Task
This is the third problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. The first, Running to school, does not require that the unit fractions that comprise 3/4 be subdivided in order to find 1/3 of 3/4. The second task, Drinking Juice, does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. This task also requires subdivision and involves multiplying a fraction and a mixed number.
Type: Problem-Solving Task
The purpose of this task is to gain a better understanding of multiplying with fractions. Students should use the diagram provided to support their findings.
Type: Problem-Solving Task
This problem helps students gain a better understanding of multiplying with fractions.
Type: Problem-Solving Task
The purpose of this task is to provide students with a concrete experience they can relate to fraction multiplication. Perhaps more importantly, the task also purposefully relates length and locations of points on a number line, a common trouble spot for students. This task is meant for instruction and would be a useful as part of an introductory unit on fraction multiplication.
Type: Problem-Solving Task
This is the second problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. This task does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2.
Type: Problem-Solving Task
The purpose of this task is to have students think about the meaning of multiplying a number by a fraction, and use this burgeoning understanding of fraction multiplication to make sense of the commutative property of multiplication in the case of fractions.
Type: Problem-Solving Task
Tutorials
In this tutorial, the four operations are applied to fractions with the visualization of the number line. This tutorial starts by adding fractions with the same denominators and explains the logic behind multiplication of fractions. This tutorial also highlights the application and extension of previous understandings of mulitplication to multiply a fraction or whole number by a fraction.
a. Interpret the product (a/b) x q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a x q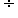 b. In general, (a/b) x (c/d) = ac/bd.
b. In general, (a/b) x (c/d) = ac/bd.
Type: Tutorial
The video describes how to multiply fractions and state the answer in lowest terms.
Type: Tutorial
Parent Resources
Problem-Solving Tasks
The purpose of this task is for students to find the answer to a question in context that can be represented by fraction multiplication. This task is appropriate for either instruction or assessment depending on how it is used and where students are in their understanding of fraction multiplication.
Type: Problem-Solving Task
This tasks lends itself very well to multiple solution methods. Students may learn a lot by comparing different methods. Students who are already comfortable with fraction multiplication can go straight to the numeric solutions given below. Students who are still unsure of the meanings of these operations can draw pictures or diagrams.
Type: Problem-Solving Task
The task could be one of the first activities for introducing the multiplication of fractions. The task has fractions which are easy to draw and provides a linear situation. Students benefit from reasoning through the solution to such word problems before they are told that they can be solved by multiplying the fractions; this helps them develop meaning for fraction multiplication.
Type: Problem-Solving Task
This is the third problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. The first, Running to school, does not require that the unit fractions that comprise 3/4 be subdivided in order to find 1/3 of 3/4. The second task, Drinking Juice, does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. This task also requires subdivision and involves multiplying a fraction and a mixed number.
Type: Problem-Solving Task
The purpose of this task is to gain a better understanding of multiplying with fractions. Students should use the diagram provided to support their findings.
Type: Problem-Solving Task
This problem helps students gain a better understanding of multiplying with fractions.
Type: Problem-Solving Task
The purpose of this task is to provide students with a concrete experience they can relate to fraction multiplication. Perhaps more importantly, the task also purposefully relates length and locations of points on a number line, a common trouble spot for students. This task is meant for instruction and would be a useful as part of an introductory unit on fraction multiplication.
Type: Problem-Solving Task
This is the second problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. This task does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2.
Type: Problem-Solving Task
The purpose of this task is to have students think about the meaning of multiplying a number by a fraction, and use this burgeoning understanding of fraction multiplication to make sense of the commutative property of multiplication in the case of fractions.
Type: Problem-Solving Task
Tutorial
The video describes how to multiply fractions and state the answer in lowest terms.
Type: Tutorial








