Clarifications
Clarification 1: Instruction includes constructing two-column proofs, pictorial proofs, paragraph and narrative proofs, flow chart proofs or informal proofs.Clarification 2: Instruction focuses on helping a student choose a method they can use reliably.
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
- MA.912.GR.2.6
- MA.912.GR.2.7
- MA.912.GR.2.8
- MA.912.GR.2.9
- MA.912.GR.5
- MA.912.T.1.1
- MA.912.T.1.2
- MA.912.T.1.3
- MA.912.T.1.4
- MA.912.LT.4.3
- MA.912.LT.4.8
- MA.912.LT.4.10
Terms from the K-12 Glossary
- Angle
- Congruent
- Corresponding Angles
- Hypotenuse
- Right Triangle
- Similarity
- Triangle
- Vertical Angles
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students were introduced to the concepts of congruence and similarity using transformations and proportional relationships. In Geometry, students prove triangle congruence or similarity using Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), Angle-Angle-Side (AAS), Angle-Angle (AA) and Hypotenuse-Leg (HL) criteria. In later courses, these congruence and similarity criteria are critical in understanding applications of vectors and trigonometry.- Students should develop the understanding of which criteria can be used to prove congruence and which criteria should be used to prove similarity.
- Criteria that can be used to prove congruence are SSS, SAS, ASA, AAS and HL, where the assumption is that the respective sides in the criterion are equal in length, and the respective angles are equal in measure.
- Criteria that can be used to prove similarity are AA, SAS and SSS, where the assumption is that the respective sides in the criterion are proportional in length with the same constant of proportionality, and the respective angles are equal in measure.
- Instruction includes developing the understanding that congruence implies similarity. Students should realize that if they have proved congruence of two triangles, then they have also proved similarity of the two triangles.
- Instruction includes the connection to the Logic and Discrete Theory benchmarks when developing proofs. Additionally, with the construction of proofs, instruction reinforces the Properties of Operations, Equality and Inequality. (MTR.5.1)
- Instruction utilizes different ways students can organize their reasoning by constructing various proofs when proving geometric statements. It is important to explain the terms statements and reasons, their roles in a geometric proof, and how they must correspond to each other. Regardless of the style, a geometric proof is a carefully written argument that begins with known facts, proceeds from there through a series of logical deductions, and ends with the statement you are trying to prove. (MTR.2.1)
- For examples of different types of proofs, please see MA.912.LT.4.8.
- Instruction includes the use of hatch marks, hash marks, arc marks or tick marks, a form of mathematical notation, to represent segments of equal length or angles of equal measure in diagrams and images.
- Students should understand the difference between congruent and equal. If two segments are congruent (i.e., PQ ≅ MN), then they have equivalent lengths (i.e., PQ = MN) and the converse is true. If two angles are congruent (i.e., ∠ABC ≅ ∠PQR), then they have equivalent angle measure (i.e., ∠ABC = ∠PQR) and the converse is true.
- Problem types include mathematical or real-world context where students identify which one of the congruence or similarity criteria can be applied in specific cases; deduce information (e.g., vertical angles are congruent, reflexive property for a shared side or angle, corresponding angles when two parallel lines are cut by a transversal are congruent) from given images to determine the congruence or similarity criterion needed to prove triangle congruence or similarity; and determine what piece of information about a pair of triangles must be added to prove triangles are congruent or similar by a certain criterion. (MTR.6.1)
- Instruction includes exploring why Hypotenuse-Leg (HL) can be used to show right triangles are congruent. Students should be able to realize that HL is a specific case of Side-Side-Side (SSS) and Side-Angle-Side (SAS) applying the Pythagorean Theorem.
- Instruction for some theorems, relationships or postulates may be necessary in order to prove the validity of congruence or similarity criteria.
- For example, to prove the validity of the AA similarity criterion, students will need knowledge of the Triangle Sum Theorem.
Common Misconceptions or Errors
- Students may confuse the congruence and similarity versions of the Side-Side-Side and Side-Angle-Side criteria. To address this misconception, provide students with counterexamples and opportunities to discuss the difference.
- Students may try to use Angle-Angle, Angle-Angle-Angle or Side-Side-Angle to prove congruence
Instructional Tasks
Instructional Task 1 (MTR.4.1, MTR.5.1)- Pentagon ABCDE, as shown below, is a regular pentagon.
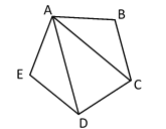
- Part A. Can you identify two possible congruent triangles in the figure?
- Part B. Write a congruence statement for the two triangles that are congruent.
- Part C. What theorem or postulate can be used to prove the two triangles congruent?
- Part D. Prove that the two triangles chosen in Part A are congruent to one another.
- Part E. Determine a triangle that is congruent to triangle ACD.
- Part F. Repeat Parts B through D with the new pair of triangles.
Instructional Task 2 (MTR.4.1, MTR.5.1)
- Part A. Draw a triangle with side lengths 6 inches, 7 inches and 10 inches. Compare your triangle with a partner.
- Part B. Draw a triangle with side lengths 4 inches and 6 inches, and with a 70° angle in between those side lengths. Compare your triangle with a partner.
- Part C. Draw a triangle with angle measures of 40° and 60°, and a side length of 5 inches between those angle measures. Compare your triangle with a partner.
- Part D. Based on the comparison of triangles created from Parts A, B and C, what can you conclude about criteria for determining triangle congruence?
Instructional Items
Instructional Item 1- Use rectangle ABCD to fill in the blanks.
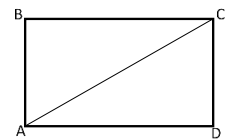
In a rectangle opposite sides are _______ which means ¯ ≅ ¯ . Triangles ABC and CDA can be proven congruent by Hypotenuse-Leg because _____ is the hypotenuse for both triangles.
Related Courses
Related Access Points
Related Resources
Formative Assessments
Lesson Plans
Perspectives Video: Teaching Idea
Problem-Solving Tasks
MFAS Formative Assessments
Students are asked to draw a triangle with given angle measures, and explain if these conditions determine a unique triangle.
Students are asked to draw a triangle given the measures of two angles and a non-included side and to explain if these conditions determine a unique triangle.
Students are asked to draw a triangle given the measures of two angles and their included side and to explain if these conditions determine a unique triangle.
Students are asked to draw a triangle given the measures of two sides and their included angle and to explain if these conditions determine a unique triangle.
Students are asked to draw a triangle given the lengths of two of its sides and the measure of a nonincluded angle and to decide if these conditions determine a unique triangle.
Students are asked to justify statements of a proof of the AA Similarity Theorem.
Students are asked locate a pair of similar triangles in a diagram, explain why they are similar, and use the similarity to find two unknown lengths in the diagram.
Students are asked to locate a pair of similar triangles in a diagram, explain why they are similar, and use the similarity to find an unknown length in the diagram.
Students are asked to write an informal justification of the AA Similarity Theorem.
Student Resources
Problem-Solving Tasks
Using a triangle with line through it, students are tasked to show the congruent angles, and conclude if one triangle is similar to the other.
Type: Problem-Solving Task
This problem solving task asks students to find the area of a triangle by using unit squares and line segments.
Type: Problem-Solving Task
This problem solving task ask students to show the reflection of one triangle maps to another triangle.
Type: Problem-Solving Task
In this problem, we considered SSA. The triangle congruence criteria, SSS, SAS, ASA, all require three pieces of information. It is interesting, however, that not all three pieces of information about sides and angles are sufficient to determine a triangle up to congruence.
Type: Problem-Solving Task
This is a reasonably direct task aimed at having students use previously-derived results to learn new facts about parallelograms, as opposed to deriving them from first principles.
Type: Problem-Solving Task
This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context.
Type: Problem-Solving Task
This problem solving task challenges students to construct a perpendicular bisector of a given segment.
Type: Problem-Solving Task
This problem solving task challenges students to explain the reason why the given triangles are congruent, and to construct reflections of the points.
Type: Problem-Solving Task
This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected.
Type: Problem-Solving Task
This problem solving task asks students to explain certain characteristics about a triangle.
Type: Problem-Solving Task
This particular problem solving task exhibits congruency between two triangles, demonstrating translation, reflection and rotation.
Type: Problem-Solving Task
The purpose of this task is primarily assessment-oriented, asking students to demonstrate knowledge of how to determine the congruency of triangles.
Type: Problem-Solving Task
This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts.
Type: Problem-Solving Task
This problem solving task focuses on a remarkable fact which comes out of the construction of the inscribed circle in a triangle: the angle bisectors of the three angles of triangle ABC all meet in a point.
Type: Problem-Solving Task
The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem.
Type: Problem-Solving Task
Parent Resources
Problem-Solving Tasks
Using a triangle with line through it, students are tasked to show the congruent angles, and conclude if one triangle is similar to the other.
Type: Problem-Solving Task
This problem solving task asks students to find the area of a triangle by using unit squares and line segments.
Type: Problem-Solving Task
This problem solving task ask students to show the reflection of one triangle maps to another triangle.
Type: Problem-Solving Task
In this problem, we considered SSA. The triangle congruence criteria, SSS, SAS, ASA, all require three pieces of information. It is interesting, however, that not all three pieces of information about sides and angles are sufficient to determine a triangle up to congruence.
Type: Problem-Solving Task
This is a reasonably direct task aimed at having students use previously-derived results to learn new facts about parallelograms, as opposed to deriving them from first principles.
Type: Problem-Solving Task
This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context.
Type: Problem-Solving Task
This problem solving task challenges students to construct a perpendicular bisector of a given segment.
Type: Problem-Solving Task
This problem solving task challenges students to explain the reason why the given triangles are congruent, and to construct reflections of the points.
Type: Problem-Solving Task
This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected.
Type: Problem-Solving Task
This problem solving task asks students to explain certain characteristics about a triangle.
Type: Problem-Solving Task
This particular problem solving task exhibits congruency between two triangles, demonstrating translation, reflection and rotation.
Type: Problem-Solving Task
The purpose of this task is primarily assessment-oriented, asking students to demonstrate knowledge of how to determine the congruency of triangles.
Type: Problem-Solving Task
This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts.
Type: Problem-Solving Task
This problem solving task focuses on a remarkable fact which comes out of the construction of the inscribed circle in a triangle: the angle bisectors of the three angles of triangle ABC all meet in a point.
Type: Problem-Solving Task
The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem.
Type: Problem-Solving Task