Given a table, equation or graph that represents a function, create a corresponding table, equation or graph of the transformed function defined by adding a real number to the x- or y-values or multiplying the x- or y-values by a real number.
General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Functions
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
- MA.912.AR.2.4
- MA.912.AR.2.5
- MA.912.AR.3.7
- MA.912.AR.3.8
- MA.912.AR.4.4
- MA.912.AR.5.6
- MA.912.AR.5.7
- MA.912.AR.5.8
- MA.912.AR.5.9
- MA.912.F.1.1
Terms from the K-12 Glossary
- Transformation
- Translation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students performed single transformations on two-dimensional figures. In Algebra I, students identified the effects of single transformations on linear, quadratic and absolute value functions. In Geometry, students performed multiple transformations on two-dimensional figures. In Mathematics for College Algebra, students identify effects of transformations on linear, quadratic, exponential, logarithmic and absolute value functions.- In this benchmark, students will create a table, equation or graph of a transformed function defined by adding a real number to the -or -values or multiplying the -or -values by a real number.
- Instruction includes the use of a graphic software to ensure adequate time for students to examine multiple transformations on the graphs of functions.
- Given a function , the transformed function () = ( − ) is a horizontal shift of (). Adding a real number, , to all the inputs (-values) of a function will result in shifting the output left or right depending on the sign of . If > is positive, the graph will shift right. If is negative, the graph will shift left.
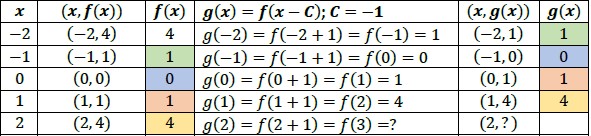
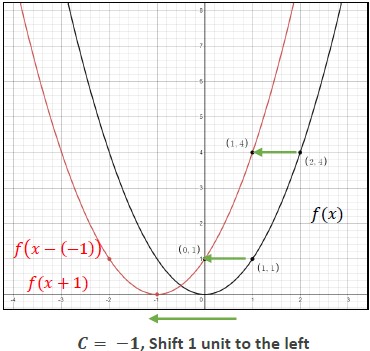
- Given a function , the transformed function () = () + is a vertical shift of (). Adding a real number, , to all the outputs (-values) of a function will result in shifting the output up or down depending on the sign of . If is positive the graph will shift up, and if is negative the graph will shift down.
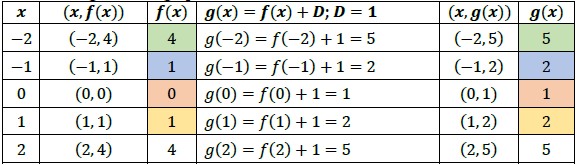
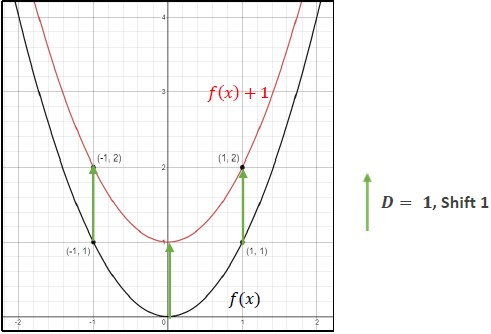
- Discuss with the students that as well as translations of two-dimensional figures, adding a constant to either the input or output of a function change the position of the graph, but it doesn’t change the shape of the graph (MTR.4.1).
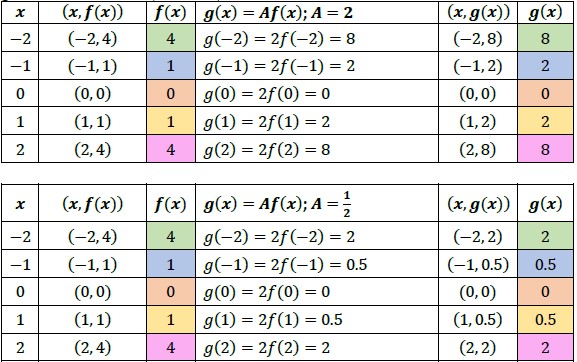
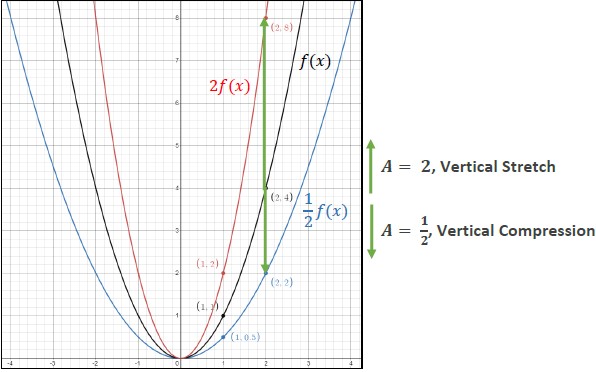
- Given a function , the transformed function () = () is a vertical stretch or compression of (). Multiplying all the outputs (-values) of a function by a real number, , will result in a vertical stretching or compression depending on the value of . If is between 0 and 1 (0 < < 1), the graph will be vertically compressed and if is greater than 1 ( > 1), the graph will be vertically stretched.
- If is a negative number ( < 0), the transformed graph will be a combination of a vertical stretch or compression and a reflection over the -axis. Discuss with students how multiplying all the -values by −1 is the same as reflecting a two-dimensional figure over the -axis (MTR.4.1).
- Given a function , the transformed function () = () is a horizontal stretch or compression of (). Multiplying all the inputs (-values) of a function by a real number, , will result in a horizontal stretching or compression depending on the value of . If is between 0 and 1 (0 < <1), the graph will be horizontally stretched by and if
B B 1 B - If
B B y x y 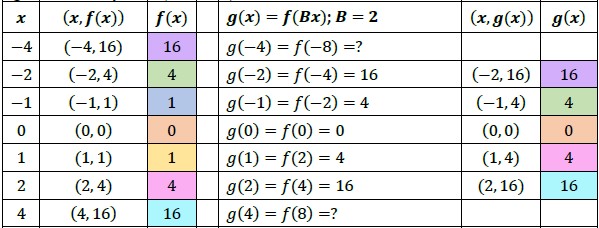
- Discuss with students the meaning of
g x f x g x f x 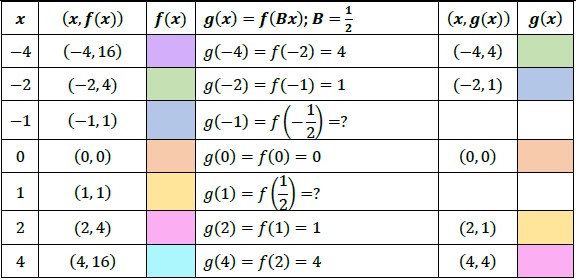
- Discuss with students the meaning of
g x f 1 2 x g x f x g f 1 2 f 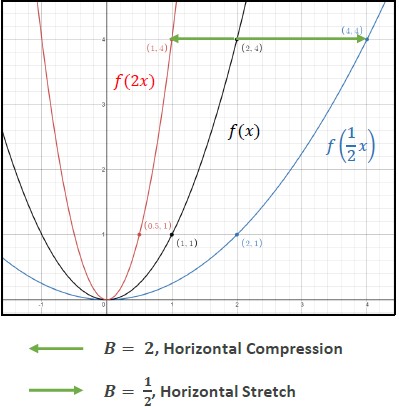
Common Misconceptions or Errors
- Some students may have difficulty seeing the impact of a transformation when comparing tables and graphs. In these cases, encourage students to convert the graph to a second table, using the same domain as the first table. This should aid in comparisons (MTR.2.1).
- Some students misinterpret how the parameters of the equation of a transformed function are affected by a horizontal translation. This may indicate that students do not understand the relationship between the graph and the equation of the function.
- For example, a student may think that
g x f x x f x x C
- For example, a student may think that
- Some students may have difficulties understanding that multiplying the input of a function by a number greater than 1 will result in a horizontal compression of the graph instead of a stretching. It is important to point out that multiplying the
x f x B x B B
Instructional Tasks
Instructional Task 1 (MTR.2.1)- The figure shows the graph of a function
f x 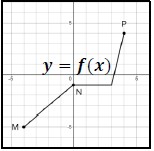
- Part A: Sketch the graph of each transformation described below and compare it with the graph of
f
a.g x f x
b.h x f x
c.k x f x
d.r x f x - Part B: The points labeled
M N P f M N P M N P g h k r 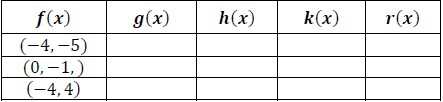
Instructional Items
Instructional Item 1 (MTR.3.1)- Given the function
f x x f x g x f x x g x
Instructional Item 2 (MTR.3.1)
- Given the function
f x f x g x f x g x f x
Instructional Item 3 (MTR.3.1)
- A function
f x
a.g x f x
b.h x f x 
Related Courses
This benchmark is part of these courses.
1200330: Algebra 2 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
1200340: Algebra 2 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7912095: Access Algebra 2 (Specifically in versions: 2016 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current))
1200710: Mathematics for College Algebra (Specifically in versions: 2022 - 2024, 2024 and beyond (current))
Related Access Points
Alternate version of this benchmark for students with significant cognitive disabilities.
MA.912.F.2.AP.5: Given a table, equation or graph that represents a function, select a corresponding table, equation or graph of the transformed function defined by adding a real number to the x- or y-values.
Related Resources
Vetted resources educators can use to teach the concepts and skills in this benchmark.
Original Student Tutorial
Original Student Tutorials Mathematics - Grades 9-12
Dilations...The Effect of k on a Graph:
Visualize the effect of using a value of k in both kf(x) or f(kx) when k is greater than zero in this interactive tutorial.
Student Resources
Vetted resources students can use to learn the concepts and skills in this benchmark.
Original Student Tutorial
Dilations...The Effect of k on a Graph:
Visualize the effect of using a value of k in both kf(x) or f(kx) when k is greater than zero in this interactive tutorial.
Type: Original Student Tutorial
Parent Resources
Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.








