Word (.docx)
Acrobat (.pdf)
Clarifications
Clarification 1: Instruction develops the understanding that there could be no line of symmetry, exactly one line of symmetry or more than one line of symmetry.Clarification 2: Instruction includes folding paper along a line of symmetry so that both halves match exactly to confirm line-symmetric figures.
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Line of Symmetry
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to draw lines of symmetry and identify line- symmetric figures. In Grade 2, students identify lines of symmetry in a two-dimensional figure by partitioning (e.g., folding) it and matching its halves. In addition, students in Grade 3 also developed the understanding that a figure can have no lines of symmetry, exactly 1 line of symmetry, or more than 1 line of symmetry.- During instruction, teachers should continue encouraging students to partition figures and match their halves to identify line(s) of symmetry (MTR.2.1).
- Instruction can also ask students to build generalizations about which two-dimensional figures are line symmetric and why. For example, students could argue that all squares share similar defining attributes and only differ in size, therefore all squares will be line- symmetric (MTR.2.1, MTR.4.1).
- Instruction builds a foundation for exploring reflections in middle school.
Common Misconceptions or Errors
- Students can miss identifying all lines of symmetry in line-symmetric figures. Encourage classroom discussions and have students justify their arguments about lines of symmetry using their partitioned representations.
Strategies to Support Tiered Instruction
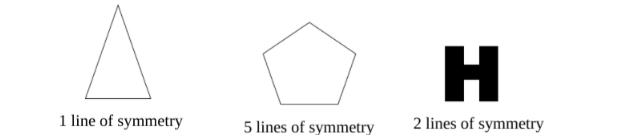
- Teacher provides figures that have at least one line of symmetry and tells how many lines of symmetry the figure has. Students draw lines to show where the lines of symmetry would be.
- For example, the teacher provides students with images similar to those shown below and has students draw the number of lines of symmetry given and explain how they know the lines they draw are lines of symmetry.
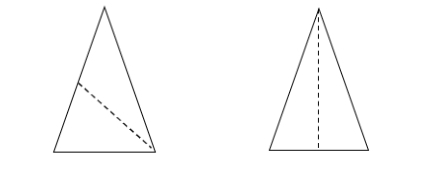
- Teacher provides a figure partitioned in different ways with dotted lines. Students fold the image along the dotted line and determine if it is a line of symmetry (do the two sides match).
- For example, the teacher gives a triangle like the one shown below. Students fold along the dotted lines and determine if it shows a line of symmetry or not.
Instructional Tasks
Instructional Task 1
Mika says that the uppercase letter H below has 1 line of symmetry. Errol says that the uppercase letter H has 2 lines of symmetry. Who is correct? Show your thinking.
Instructional Task 2
Determine if the figure below has 0 lines of symmetry, 1 line of symmetry, or more than 1 line of symmetry. Explain your thinking.
Instructional Items
Instructional Item 1
Select all the figures that have at least one line of symmetry.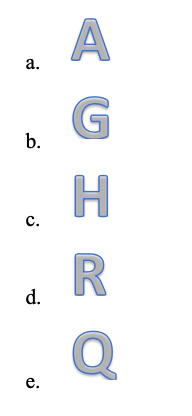
Instructional Item 2
How many lines of symmetry does the following figure have?
Instructional Item 3
A figure is shown. How many lines of symmetry does the figure have?
Instructional Item 4
Draw the lines of symmetry on the figure below.
Instructional Item 5
In which figure is the line of symmetry NOT drawn correctly?
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
Related Access Points
Related Resources
Formative Assessments
Image/Photograph
Lesson Plans
Original Student Tutorial
Problem-Solving Tasks
STEM Lessons - Model Eliciting Activity
Rangoli is a traditional Indian art that is used in decorating the entrance of the house to welcome guests. In this activity students will use the concept of lines of symmetry to select the best rangoli design for a school event.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought processes. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEAs visit: https://www.cpalms.org/cpalms/mea.aspx
MFAS Formative Assessments
Students are asked to determine if lines drawn on two-dimensional figures are lines of symmetry and to explain their decisions.
Students are asked to identify line-symmetric figures and then draw the lines of symmetry.
Students are asked to determine how many lines of symmetry a square has by drawing the lines of symmetry. Students then consider whether all quadrilaterals have four lines of symmetry.
Students are asked to use a line of symmetry to complete a drawing. Additionally, they consider how to describe a line of symmetry.
Original Student Tutorials Mathematics - Grades K-5
Help the Symmetry Sisters save the City of Symmetry Line and the State of Arithmetic from the Radical Rat in this interactive tutorial!
Student Resources
Original Student Tutorial
Help the Symmetry Sisters save the City of Symmetry Line and the State of Arithmetic from the Radical Rat in this interactive tutorial!
Type: Original Student Tutorial
Problem-Solving Tasks
This activity provides students an opportunity to recognize these distinguishing features of the different types of triangles before the technical language has been introduced. For finding the lines of symmetry, cut-out models of the four triangles would be helpful so that the students can fold them to find the lines.
Type: Problem-Solving Task
This task provides students a chance to experiment with reflections of the plane and their impact on specific types of quadrilaterals. It is both interesting and important that these types of quadrilaterals can be distinguished by their lines of symmetry.
Type: Problem-Solving Task
This is an instructional task that gives students a chance to reason about lines of symmetry and discover that a circle has an an infinite number of lines of symmetry. Even though the concept of an infinite number of lines is fairly abstract, students can understand infinity in an informal way.
Type: Problem-Solving Task
Parent Resources
Image/Photograph
In this lesson, you will find clip art and various illustrations of polygons, circles, ellipses, star polygons, and inscribed shapes.
Type: Image/Photograph
Problem-Solving Tasks
This activity provides students an opportunity to recognize these distinguishing features of the different types of triangles before the technical language has been introduced. For finding the lines of symmetry, cut-out models of the four triangles would be helpful so that the students can fold them to find the lines.
Type: Problem-Solving Task
This task provides students a chance to experiment with reflections of the plane and their impact on specific types of quadrilaterals. It is both interesting and important that these types of quadrilaterals can be distinguished by their lines of symmetry.
Type: Problem-Solving Task
This is an instructional task that gives students a chance to reason about lines of symmetry and discover that a circle has an an infinite number of lines of symmetry. Even though the concept of an infinite number of lines is fairly abstract, students can understand infinity in an informal way.
Type: Problem-Solving Task
