Related Benchmarks
Related Access Points
Access Points
Related Resources
Formative Assessments
Lesson Plans
Original Student Tutorials
Perspectives Video: Experts
Problem-Solving Tasks
Video/Audio/Animation
Student Resources
Original Student Tutorials
Use scientific notation to compare the distances of planets and other objects from the Sun in this interactive tutorial.
Type: Original Student Tutorial
Use astronomical units to compare distances betweeen objects in our solar system in this interactive tutorial.
Type: Original Student Tutorial
Learn how to simplify radicals in this interactive tutorial.
Type: Original Student Tutorial
Explore how to express large quantities using scientific notation in this interactive tutorial.
Type: Original Student Tutorial
Apply the Pythagorean Theorem to solve mathematical and real-rorld problems in this interactive tutorial.
Type: Original Student Tutorial
Problem-Solving Tasks
This problem solving task challenges students to apply the concepts of mass, volume, and density in the real-world context to find how many cells are in the human body.
Type: Problem-Solving Task
This task is intended for instructional purposes so that students can become familiar and confident with using a calculator and understanding what it can and cannot do. This task gives an opportunity to work on the notion of place value (in parts [b] and [c]) and also to understand part of an argument for why the square root of 2 is not a rational number.
Type: Problem-Solving Task
The task assumes that students can express a given repeating decimal as a fraction. Teachers looking for a task to fill in this background knowledge could consider the related task "Converting Decimal Representations of Rational Numbers to Fraction Representations".
Type: Problem-Solving Task
When students plot irrational numbers on the number line, it helps reinforce the idea that they fit into a number system that includes the more familiar integer and rational numbers. This is a good time for teachers to start using the term "real number line" to emphasize the fact that the number system represented by the number line is the real numbers. When students begin to study complex numbers in high school, they will encounter numbers that are not on the real number line (and are, in fact, on a "number plane"). This task could be used for assessment, or if elaborated a bit, could be used in an instructional setting.
Type: Problem-Solving Task
Students are given a pair of numbers. They are asked to determine which is larger, and then justify their answer. The numbers involved are rational numbers and common irrational numbers, such p and square roots. This task can be used to either build or assess initial understandings related to rational approximations of irrational numbers.
Type: Problem-Solving Task
The student is asked to perform operations with numbers expressed in scientific notation to decide whether 7% of Americans really do eat at Giantburger every day.
Type: Problem-Solving Task
This is an instructional task meant to generate a conversation around the meaning of negative integer exponents. It is good for students to learn the convention that negative time is simply any time before t=0.
Type: Problem-Solving Task
Video/Audio/Animation
Exponentiation can be understood in terms of repeated multiplication much like multiplication can be understood in terms of repeated addition. Properties of multiplication and division of exponential expressions with the same base are derived.
Type: Video/Audio/Animation
Parent Resources
Problem-Solving Tasks
This problem solving task challenges students to apply the concepts of mass, volume, and density in the real-world context to find how many cells are in the human body.
Type: Problem-Solving Task
In this problem students are comparing a very small quantity with a very large quantity using the metric system. The metric system is especially convenient when comparing measurements using scientific notations since different units within the system are related by powers of ten.
Type: Problem-Solving Task
This task requires students to work with very large and small values expressed both in scientific notation and in decimal notation (standard form). In addition, students need to convert units of mass. The solution below converts the mass of humans into grams; however, we could just as easily converted the mass of ants into kilograms. Students are unable to go directly to a calculator without taking into account all of the considerations mentioned above. Even after converting units and decimals to scientific notation, students should be encouraged to use the structure of scientific notation to regroup the products by extending the properties of operations and then use the properties of exponents to more fluently perform the calculations involved rather than rely heavily on a calculator.
Type: Problem-Solving Task
This task is intended for instructional purposes so that students can become familiar and confident with using a calculator and understanding what it can and cannot do. This task gives an opportunity to work on the notion of place value (in parts [b] and [c]) and also to understand part of an argument for why the square root of 2 is not a rational number.
Type: Problem-Solving Task
The task assumes that students can express a given repeating decimal as a fraction. Teachers looking for a task to fill in this background knowledge could consider the related task "Converting Decimal Representations of Rational Numbers to Fraction Representations".
Type: Problem-Solving Task
When students plot irrational numbers on the number line, it helps reinforce the idea that they fit into a number system that includes the more familiar integer and rational numbers. This is a good time for teachers to start using the term "real number line" to emphasize the fact that the number system represented by the number line is the real numbers. When students begin to study complex numbers in high school, they will encounter numbers that are not on the real number line (and are, in fact, on a "number plane"). This task could be used for assessment, or if elaborated a bit, could be used in an instructional setting.
Type: Problem-Solving Task
In this task, students explore some important mathematical implications of using a calculator. Specifically, they experiment with the approximation of common irrational numbers such as pi (p) and the square root of 2 (v2) and discover how to properly use the calculator for best accuracy. Other related activities involve converting fractions to decimal form and a concrete example where rounding and then multiplying does not yield the same answer as multiplying and then rounding.
Type: Problem-Solving Task
Students are given a pair of numbers. They are asked to determine which is larger, and then justify their answer. The numbers involved are rational numbers and common irrational numbers, such p and square roots. This task can be used to either build or assess initial understandings related to rational approximations of irrational numbers.
Type: Problem-Solving Task
The student is asked to perform operations with numbers expressed in scientific notation to decide whether 7% of Americans really do eat at Giantburger every day.
Type: Problem-Solving Task
This is an instructional task meant to generate a conversation around the meaning of negative integer exponents. It is good for students to learn the convention that negative time is simply any time before t=0.
Type: Problem-Solving Task



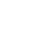



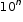 .
.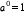 and
and 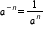
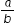 by completing an exploration worksheet. They will conclude that any number which can be written in this form is called a rational number.
by completing an exploration worksheet. They will conclude that any number which can be written in this form is called a rational number.
