MA.6.A.2.2Archived Standard

loading spinner
Export Print
Interpret and compare ratios and rates.

Remarks

Example: Jessica made 8 out of 24 free throws. Bob made 5 out of 20 free throws. Who has the highest free throw ratio?

 

Ratios may be represented in various forms such as simple drawings or multiplication tables.

General Information
Subject Area: X-Mathematics (former standards - 2008)
Grade: 6
Body of Knowledge: Algebra
Idea: Level 2: Basic Application of Skills & Concepts
Big Idea: BIG IDEA 2 - Connect ratio and rates to multiplication and division.
Date Adopted or Revised: 09/07
Content Complexity Rating: Level 2: Basic Application of Skills & Concepts - More Information
Date of Last Rating: 06/07
Status: State Board Approved - Archived
Assessed: Yes
Test Item Specifications
  • Item Type(s): This benchmark may be assessed using: MC item(s)

  • Clarification :
    Students will translate situations involving ratio and rate from real-world contexts to mathematical equations or expressions.

    Students will compare rates and ratios to solve real-world problems.
  • Content Limits :
    Items will not include defining rate and ratio.

    Items will not include inequality symbols.

    Ratios may be presented in words or symbols (e.g., 2 to 3, 2:3, 2 out of 3, or 2/3).
  • Stimulus Attributes :
    Items should be set in a real-world context.

    Ratios may be represented in various forms, such as simple drawings and multiplication tables.
Sample Test Items (1)
  • Test Item #: Sample Item 1
  • Question: Mr. Gerard purchased different types of halogen light bulbs for the apartment building where he works. The information about the bulbs he purchased is shown in the table below.

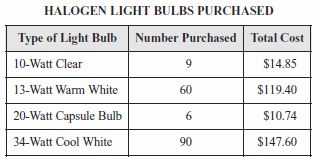
    Chart

    Which type of light bulb costs the least amount per light bulb?

  • Difficulty: N/A
  • Type: MC: Multiple Choice

Related Access Points

Alternate version of this benchmark for students with significant cognitive disabilities.

Related Resources

Vetted resources educators can use to teach the concepts and skills in this benchmark.

Perspectives Video: Professional/Enthusiast

Gear Heads and Gear Ratios:

<p>Have a need for speed? Get out your spreadsheet! Race car drivers use algebraic formulas and spreadsheets to optimize car performance.</p>

Type: Perspectives Video: Professional/Enthusiast

Problem-Solving Tasks

Ratio - Make Some Chocolate Crispies:

In this activity students calculate the ratio of chocolate to cereal when making a cake. Students then use that ratio to calculate to amount of chocolate and cereal necessary to make 21 cakes.

Type: Problem-Solving Task

Space Math - Comparing Planets Orbiting Other Stars:

This NASA lesson utilizes real world data about the size of planets orbiting other stars. Students are asked to use this data to compare the size of the planets to Earth and Jupiter. Lesson includes a visual representation and an answer key.

Type: Problem-Solving Task

Teaching Ideas

Space Math: Estimating the Speed of a Tsunami:

Students use real-world data from the 2011 Pacific Ocean earthquake and tsunami to estimate the speed of the tsunami as it crossed the Pacific Ocean. Students will also need to work through the issue of time zones and the International Date Line.

Type: Teaching Idea

Calculating Sharks-SeaWorld Classroom Activity:

  • Given data about sharks and the amount of food they eat, students will be able to solve for the unknown in percentage problems.
  • Given information about a shark's growth, students will be able to graph coordinates and interpret a linear graph.
  • Given the conversion factor, students will be able to convert from metric to English units.

Type: Teaching Idea

Virtual Manipulative

Planet Size Comparison: Ratio:

Images of two planets selected on two drop-down menus with a display of their respective diameters and the applicable ratio.

Type: Virtual Manipulative

Student Resources

Vetted resources students can use to learn the concepts and skills in this benchmark.

Parent Resources

Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.

Problem-Solving Task

Ratio - Make Some Chocolate Crispies:

In this activity students calculate the ratio of chocolate to cereal when making a cake. Students then use that ratio to calculate to amount of chocolate and cereal necessary to make 21 cakes.

Type: Problem-Solving Task