MAFS.912.G-C.1.2Archived Standard

loading spinner
Export Print
Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle.
General Information
Subject Area: Mathematics
Grade: 912
Domain-Subdomain: Geometry: Circles
Cluster: Level 2: Basic Application of Skills & Concepts
Cluster: Understand and apply theorems about circles. (Geometry - Additional Cluster) -

Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.

Date Adopted or Revised: 02/14
Content Complexity Rating: Level 2: Basic Application of Skills & Concepts - More Information
Date of Last Rating: 02/14
Status: State Board Approved - Archived
Assessed: Yes
Test Item Specifications

  • Assessment Limits :
    Items may include finding or describing the length of arcs when given
    information. 
  • Calculator :

    Neutral

  • Clarification :
    Students will solve problems related to circles using the properties of
    central angles, inscribed angles, circumscribed angles, diameters,
    radii, chords, and tangents. 
  • Stimulus Attributes :
    Items may be set in a real-world or mathematical context. 
  • Response Attributes :
    Items may require the student to use or choose the correct unit of
    measure. 
Sample Test Items (1)
  • Test Item #: Sample Item 1
  • Question:

    In the diagram shown, chords AB and CD intersect at E. The measure of 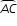begin mathsize 12px style stack A C with overparenthesis on top end style is 120º, the measure of 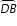begin mathsize 12px style stack D B with overparenthesis on top end style is (2x)º, and the measure of 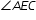begin mathsize 12px style angle A E C end style is (4x)º.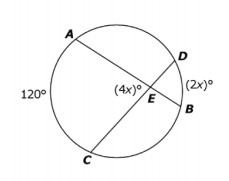

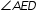    What is the degree measure of begin mathsize 12px style angle A E D end style?

  • Difficulty: N/A
  • Type: EE: Equation Editor

Related Courses

This benchmark is part of these courses.
1200400: Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206300: Informal Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated))
1206310: Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206320: Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7912060: Access Informal Geometry (Specifically in versions: 2014 - 2015 (course terminated))
1206315: Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7912065: Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current))

Related Access Points

Alternate version of this benchmark for students with significant cognitive disabilities.

Related Resources

Vetted resources educators can use to teach the concepts and skills in this benchmark.

Educational Game

Tangled Web: An Angle Relationships Game:

You are a robotic spider tangled up in an angular web. Use your knowledge of angle relationships to collect flies and teleport through wormholes to rescue your spider family!

Type: Educational Game

Formative Assessments

Central and Inscribed Angles:

Students are asked to describe the relationship between a central angle and an inscribed angle that intercept the same arc.

Type: Formative Assessment

Tangent Line and Radius:

Students are asked to draw a circle, a tangent to the circle, and a radius to the point of tangency. Students are then asked to describe the relationship between the radius and the tangent line.

Type: Formative Assessment

Inscribed Angle on Diameter:

Students are asked to find the measures of two inscribed angles of a circle.

Type: Formative Assessment

Circles with Angles:

Students are given a diagram with inscribed, central, and circumscribed angles and are asked to identify each type of angle, determine angle measures, and describe relationships among them.

Type: Formative Assessment

Lesson Plans

The Seven Circles Water Fountain:

Students will apply concepts related to circles, angles, area, and circumference to a design situation.

Type: Lesson Plan

Geometry Problems: Circles and Triangles:

This lesson unit is intended to help you assess how well students are able to use geometric properties to solve problems. In particular, the lesson will help you identify and help students who have the following difficulties:

  • Solving problems by determining the lengths of the sides in right triangles.
  • Finding the measurements of shapes by decomposing complex shapes into simpler ones.

The lesson unit will also help students to recognize that there may be different approaches to geometrical problems, and to understand the relative strengths and weaknesses of those approaches.

Type: Lesson Plan

Inscribing and Circumscribing Right Triangles:

This lesson is designed to enable students to develop strategies for describing relationships between right triangles and the radii of their inscribed and circumscribed circles.

Type: Lesson Plan

Seeking Circle Angles:

Students will start this lesson with a win-lose-draw game to review circle vocabulary words. They will then use examples on a discovery sheet to discover the relationships between arcs and the angles whose vertex is located on a circle, in the interior of the circle, and exterior to the circle. They will wrap up the lesson in a class discussion and questions answered on white boards.

Type: Lesson Plan

Seeking Circle Segments:

Students will start this lesson with a "Pictionary" game to review circle vocabulary terms. They will then use computers and GeoGebra to discover the relationships between portions of segments that intersect in the interior of the circle, and exterior to the circle. They will wrap up the lesson in a class discussion and consensus on rules (formulas).

Type: Lesson Plan

Problem-Solving Tasks

Two Wheels and a Belt:

This task combines two skills: making use of the relationship between a tangent segment to a circle and the radius touching that tangent segment, and computing lengths of circular arcs given the radii and central angles.

Type: Problem-Solving Task

Right triangles inscribed in circles II:

This problem solving task asks students to explain certain characteristics about a triangle.

Type: Problem-Solving Task

Right triangles inscribed in circles I:

This task provides a good opportunity to use isosceles triangles and their properties to show an interesting and important result about triangles inscribed in a circle: the fact that these triangles are always right triangles is often referred to as Thales' theorem.

Type: Problem-Solving Task

Tangent Lines and the Radius of a Circle:

This problem solving task challenges students to find the perpendicular meeting point of a segment from the center of a circle and a tangent.

Type: Problem-Solving Task

Neglecting the Curvature of the Earth:

This task applies geometric concepts, namely properties of tangents to circles and of right triangles, in a modeling situation. The key geometric point in this task is to recognize that the line of sight from the mountain top towards the horizon is tangent to the earth. We can then use a right triangle where one leg is tangent to a circle and the other leg is the radius of the circle to investigate this situation.

Type: Problem-Solving Task

MFAS Formative Assessments

Central and Inscribed Angles:

Students are asked to describe the relationship between a central angle and an inscribed angle that intercept the same arc.

Circles with Angles:

Students are given a diagram with inscribed, central, and circumscribed angles and are asked to identify each type of angle, determine angle measures, and describe relationships among them.

Inscribed Angle on Diameter:

Students are asked to find the measures of two inscribed angles of a circle.

Tangent Line and Radius:

Students are asked to draw a circle, a tangent to the circle, and a radius to the point of tangency. Students are then asked to describe the relationship between the radius and the tangent line.

Student Resources

Vetted resources students can use to learn the concepts and skills in this benchmark.

Problem-Solving Tasks

Two Wheels and a Belt:

This task combines two skills: making use of the relationship between a tangent segment to a circle and the radius touching that tangent segment, and computing lengths of circular arcs given the radii and central angles.

Type: Problem-Solving Task

Right triangles inscribed in circles II:

This problem solving task asks students to explain certain characteristics about a triangle.

Type: Problem-Solving Task

Right triangles inscribed in circles I:

This task provides a good opportunity to use isosceles triangles and their properties to show an interesting and important result about triangles inscribed in a circle: the fact that these triangles are always right triangles is often referred to as Thales' theorem.

Type: Problem-Solving Task

Tangent Lines and the Radius of a Circle:

This problem solving task challenges students to find the perpendicular meeting point of a segment from the center of a circle and a tangent.

Type: Problem-Solving Task

Neglecting the Curvature of the Earth:

This task applies geometric concepts, namely properties of tangents to circles and of right triangles, in a modeling situation. The key geometric point in this task is to recognize that the line of sight from the mountain top towards the horizon is tangent to the earth. We can then use a right triangle where one leg is tangent to a circle and the other leg is the radius of the circle to investigate this situation.

Type: Problem-Solving Task

Parent Resources

Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.

Problem-Solving Tasks

Two Wheels and a Belt:

This task combines two skills: making use of the relationship between a tangent segment to a circle and the radius touching that tangent segment, and computing lengths of circular arcs given the radii and central angles.

Type: Problem-Solving Task

Right triangles inscribed in circles II:

This problem solving task asks students to explain certain characteristics about a triangle.

Type: Problem-Solving Task

Right triangles inscribed in circles I:

This task provides a good opportunity to use isosceles triangles and their properties to show an interesting and important result about triangles inscribed in a circle: the fact that these triangles are always right triangles is often referred to as Thales' theorem.

Type: Problem-Solving Task

Tangent Lines and the Radius of a Circle:

This problem solving task challenges students to find the perpendicular meeting point of a segment from the center of a circle and a tangent.

Type: Problem-Solving Task

Neglecting the Curvature of the Earth:

This task applies geometric concepts, namely properties of tangents to circles and of right triangles, in a modeling situation. The key geometric point in this task is to recognize that the line of sight from the mountain top towards the horizon is tangent to the earth. We can then use a right triangle where one leg is tangent to a circle and the other leg is the radius of the circle to investigate this situation.

Type: Problem-Solving Task