Word (.docx)
Acrobat (.pdf)
Interpret a definite integral of the rate of change of a quantity over an interval as the change of the quantity over the interval. That is,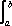 
f'(x)dx = f(b) - f(a) (fundamental theorem of calculus).
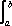f'(x)dx = f(b) - f(a) (fundamental theorem of calculus).
Remarks
Example: Explain why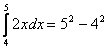
.General Information
Subject Area: Mathematics
Grade: 912
Domain-Subdomain: Calculus
Cluster: Level 3: Strategic Thinking & Complex Reasoning
Cluster: Integral Calculus - Understand that integration is used to find areas, and evaluate integrals using rectangular approximations. From this, develop the idea that integration is the inverse operation to differentiation — the Fundamental Theorem of Calculus. Use this result to find definite and indefinite integrals, including using the method of integration by substitution. Apply approximate methods, such as the Trapezoidal Rule, to find definite integrals. Define integrals using Riemann sums, use the Fundamental Theorem of Calculus to find integrals using antiderivatives, and use basic properties of integrals. Integrate by substitution, and find approximate integrals.
Date Adopted or Revised: 02/14
Content Complexity Rating:
Level 3: Strategic Thinking & Complex Reasoning
-
More Information
Date of Last Rating: 02/14
Status: State Board Approved - Archived
Related Courses
This benchmark is part of these courses.
1202300: Calculus Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
Related Access Points
Alternate version of this benchmark for students with significant cognitive disabilities.
Related Resources
Vetted resources educators can use to teach the concepts and skills in this benchmark.
Student Resources
Vetted resources students can use to learn the concepts and skills in this benchmark.
Parent Resources
Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.
