MAFS.912.C.1.7Archived Standard

loading spinner
Export Print
Decide when a limit is infinite and use limits involving infinity to describe asymptotic behavior.

Remarks

Example 1: Find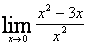 

Example 2: Where does the following function have asymptote(s)? Explain your answer.
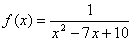
General Information
Subject Area: Mathematics
Grade: 912
Domain-Subdomain: Calculus
Cluster: Level 2: Basic Application of Skills & Concepts
Cluster: Limits and Continuity - Develop an understanding of the concept of limit by estimating limits graphically and numerically and evaluating limits analytically. Extend the idea of a limit to one-sided limits and limits at infinity. Use limits to define and understand the concept of continuity, decide whether a function is continuous at a point, and find types of discontinuities. Understand and apply continuity theorems.
Date Adopted or Revised: 02/14
Content Complexity Rating: Level 2: Basic Application of Skills & Concepts - More Information
Date of Last Rating: 02/14
Status: State Board Approved - Archived

Related Courses

This benchmark is part of these courses.
1202300: Calculus Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))

Related Access Points

Alternate version of this benchmark for students with significant cognitive disabilities.

Related Resources

Vetted resources educators can use to teach the concepts and skills in this benchmark.

Perspectives Video: Professional/Enthusiast

Asymptotic Behavior in Shark Growth Research:

Fishery Scientist from Florida State University discusses his new research in deep sea sharks and the unusual behavior that is found when the data is graphed.

Download the CPALMS Perspectives video student note taking guide.

Type: Perspectives Video: Professional/Enthusiast

Text Resource

No Limits For Usain:

This informational text resource is intended to support reading in the content area. The text uses the story of Usain Bolt and his quest to reduce his world record in the 100 meter race to raise the question of whether there is a limit to his—or any human's—athleticism. The article uses number series, limits, and convergent and divergent series to prove that, hypothetically at least, a world record will go on reducing beyond any limit. A logistic curve is shown to model the data.

Type: Text Resource

Tutorials

More Limits at Infinity:

Here we will explore three more functions, and find their limits as they approach infinity.

Type: Tutorial

Limits with Two Horizontal Asymptotes:

Here we will find the limit of a function as it approaches positive and negative infinity and results in two horizontal asymptotes.

Type: Tutorial

Limits and Infinity:

We will look at examples of limits at infinity.

Type: Tutorial

Student Resources

Vetted resources students can use to learn the concepts and skills in this benchmark.

Tutorials

More Limits at Infinity:

Here we will explore three more functions, and find their limits as they approach infinity.

Type: Tutorial

Limits with Two Horizontal Asymptotes:

Here we will find the limit of a function as it approaches positive and negative infinity and results in two horizontal asymptotes.

Type: Tutorial

Limits and Infinity:

We will look at examples of limits at infinity.

Type: Tutorial

Parent Resources

Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.