Word (.docx)
Acrobat (.pdf)
Interpret a definite integral as a limit of Riemann sums. Calculate the values of Riemann sums over equal subdivisions using left, right and midpoint evaluation points.
Examples
Example: Find the values of the Riemann sums over the interval [0,1] using 12 and 24 subintervals of equal width for f(x)=ex evaluated at the midpoint of each subinterval. Write an expression for the Riemann sums using n intervals of equal width. Find the limit of this Riemann Sums as n goes to infinity.Example: Estimate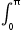
sin x dx using a Riemann midpoint sum with 4 subintervals.
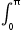sin x dx using a Riemann midpoint sum with 4 subintervals.Example: Find an approximate value for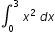 
using 6 rectangles of equal width under the graph of f(x)=x2 between x=0 and x=3. How did you form your rectangles? Compute this approximation three times using at least three different methods to form the rectangles.
General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Calculus
Date Adopted or Revised: 08/20
Status: State Board Approved
Related Courses
This benchmark is part of these courses.
1202300: Calculus Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
Related Access Points
Alternate version of this benchmark for students with significant cognitive disabilities.
Related Resources
Vetted resources educators can use to teach the concepts and skills in this benchmark.
Student Resources
Vetted resources students can use to learn the concepts and skills in this benchmark.
Parent Resources
Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.
