Construct logical arguments using laws of detachment, syllogism, tautology, contradiction and Euler Diagrams.
General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Logic and Discrete Theory
Standard: Develop an understanding of the fundamentals of propositional logic, arguments and methods of proof.
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In Geometry, students learned to construct proofs for many of the geometric facts that they encountered and learned to use counterexamples to check the validity of arguments and statements. In Math for College Liberal Arts, students learn to construct logical arguments using valid and invalid argument forms, truth tables to form tautologies and Euler Diagrams.- Instruction includes the definition of a logical argument. A logical argument consists of
given statements, called premises, and a conclusion. The premises present evidence or
reasons in support of the conclusion.
- In English, conclusion-indicator words include therefore, thus, hence, consequently, so and others that indicate that a conclusion is being made. Once the conclusion statement is identified, the remaining statements are considered premises.
- In symbolic form, the three-dot triangle, ∴ , indicates the conclusion. Moreover, a
bar,
 , is used to separate premises from the conclusion, much like an equal
sign in a vertical addition problem.
, is used to separate premises from the conclusion, much like an equal
sign in a vertical addition problem. - Making a connection to MA.912.LT.4.1, instruction presents an example of an argument composed of two premises and a conclusion, where simple statements p, q & r are defined as follows:
p : I upgrade my computer.
q : My computer will run faster.
r : I will be more productive.

- Law of Detachment, also known as direct reasoning, allows you to “detach” the premise
from the conclusion. The law provides the truth value of conditional statements. If the
conditional statement and the premise are true, then the conclusion is also true. The Law
of Detachment states that if p → q is true and p is true, then q is true.
- For example, if p → q is: If I upgrade my computer, then it will run faster and this statement is true, as well as the statement “I upgrade my computer” is true, then using the Law of Detachment, I can conclude, “My computer will run faster” is true.
- A tautology is a compound statement that is always true, regardless of the truth values of
its individual statements.
- For example, the compound statement It will rain today, or it will not rain today is always true.
- Law of Syllogism states that if p → q and q → r, then p → r is true. This logic is similar
to transitive property of equality referenced in Appendix D.
- An example for Law of Syllogism is shown below.
If p → q is: If I upgrade my computer, then it will run faster.
And q → r is: If my computer runs faster, then I will be more productive.
Then p → r is: If I upgrade my computer, then I will be more productive.
If the two statements are true, then the conclusion is also true.
- An example for Law of Syllogism is shown below.
- Contradiction is a compound statement that is always false.
- For example, the compound statement It will rain today, and it will not rain today is always false.
- Instruction includes the definition of Euler (pronounced as “oiler”) Diagrams in relation to Venn Diagrams for four types of quantified statements (MTR.2.1). Building on their knowledge of Venn Diagrams and quantified statements (MA.912.LT.4.1), students engage in discussion to reason about and connect multiple representations of the quantified statements.
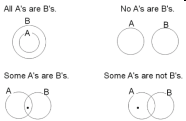
- For enrichment of this benchmark, instruction reinforces the connection between a tautology and a contradiction: a statement that is always true, regardless of the truth values of the composite simple statements, is a tautology; whereas, a statement that is always false – is called a contradiction. Students engage in discussions to highlight the difference between the two concepts (MTR.4.1).
Common Misconceptions or Errors
- Students may confuse the different types of logical arguments, specifically, the Law of Detachment and Law of Syllogism.
- Students may assume that every conclusion is a valid conclusion because it is part of a given argument. To address this, help students understand that a conclusion is logical or valid only if it forms a valid argument; thus, to determine whether a conclusion is valid, we must apply the methods learned to judge the validity of a given argument in tandem with MA.912.LT.4.10.
Instructional Tasks
Instructional Task 1 (MTR.4.1)- Part A. Construct four logical arguments.
- Part B. Create two examples of an argument using the Law of Syllogism.
Instructional Task 2 (MTR.4.1)
- Is the statement “If war is peace, then war is not peace” a tautology? Is it a contradiction? Justify your answer.
Instructional Task 3 (MTR.5.1)
- Draw two Euler diagrams to represent the possible relationships between insects and birds. All birds have wings.
Some insects have wings.
Therefore ___________.
Instructional Items
Instructional Item 1- Construct a valid argument using the Law of Detachment given the statements. I will go to Publix Monday.
Today is Monday.
Related Courses
This benchmark is part of these courses.
7912070: Access Mathematics for Liberal Arts (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 - 2023, 2023 and beyond (current))
1207350: Mathematics for College Liberal Arts (Specifically in versions: 2022 - 2024, 2024 and beyond (current))
1212300: Discrete Mathematics Honors (Specifically in versions: 2022 - 2024, 2024 and beyond (current))
Related Access Points
Alternate version of this benchmark for students with significant cognitive disabilities.
Related Resources
Vetted resources educators can use to teach the concepts and skills in this benchmark.
Student Resources
Vetted resources students can use to learn the concepts and skills in this benchmark.
Parent Resources
Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.






