Clarifications
Clarification 1: Within this benchmark, the expectation is not to find unknown side lengths.Clarification 2: Two-dimensional figures cannot exceed 12 units by 12 units and responses include the appropriate units in word form.
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Perimeter
- Rectangle
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to solve mathematical and real-world problems using the perimeter and area of rectangles using a visual model and/or a formula for each.- In the provided mathematical and real-world problems, instruction should include cases where students use a ruler to measure lengths before determining its perimeter and/or area (MTR.3.1).
- Mathematical problems include visual models of rectangles, while examples of real- world problems could include photos or classroom objects (e.g., measuring the area of one face on a tissue box). Students will not be expected to find unknown side lengths until Grade 4 (MTR.7.1).
- This benchmark gives students the chance to measure perimeter and area together and understand their differences – perimeter as a one-dimensional length measurement and area as a two-dimensional measurement. (Note: Though students explored and measured perimeter in Grade 2, they were not expected to determine a formula.) (MTR.5.1)
- As recommended for MA.3.GR.2.2 for a multiplication formula for area, classroom instruction should include activities that allow students to build formulas for perimeter based on patterns they observe (e.g., = + + + , = 2 + 2) before expecting them to memorize. Student-created formulas will build conceptual understanding around a formula before memorizing it (MTR.4.1).
Common Misconceptions or Errors
- Students may confuse area and perimeter and use incorrect formulas to find measurements. During instruction, the teacher should continue to emphasize the difference between perimeter as a one-dimensional measurement of length and area as a two-dimensional measurement that covers a shape with unit squares. The teacher can use visuals to show the perimeter (e.g., yarn, string stretched around the rectangle) and area (e.g., square counters, square-shaped sticky notes, square-shaped crackers covering it) to help students differentiate between the measurements.
Strategies to Support Tiered Instruction
- Instruction includes opportunities to explore both area and perimeter of given figures and make connections to the formulas to find each. The teacher provides students with dimensions for a figure that has whole number side lengths that can be measured using inches or centimeters. Students use a ruler to measure the side lengths and place tick marks for each whole number unit. Students then label each side length and use the formula for perimeter to calculate. Next, students use the formula for area to find the area and then use the tick marks made when measuring to draw in the rows and columns to check their work.
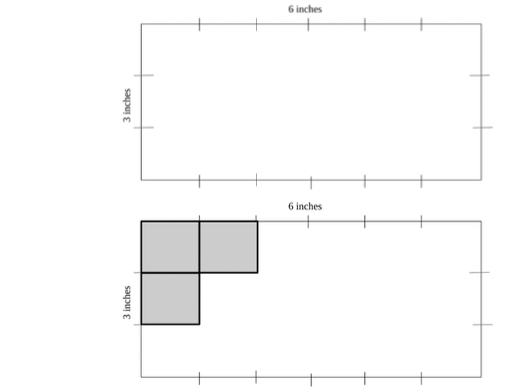
- For example, the teacher asks students to draw a figure with a length of 3 inches and a width of 6 inches. Students use a ruler to draw the figure and place tick marks along each side for each inch. Students then use the formula to find the perimeter ( = 3 + 3 + 6 + 6). Next, students use the tick marks made when measuring to draw in the rows and columns to cover the figure with square inches and then use the formula to find area ( = 3 × 6).
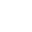
- Teacher provides a figure that has whole number side lengths that can be measured using inches. Students use a visual representation such as string or yarn to measure the distance around the figure and then measure the length of the string to make the connection to perimeter being a one-dimensional measurement. Students then use a different visual representation such as 1-inch tiles or square sticky notes to cover the figure to find the area and make the connection to area being a two-dimensional measurement.
- For example, the teacher provides an image like the example below. Students use a piece of string to measure the distance around the figure and then use a tape measure to measure the length of the string. Or students can use the string to measure the 2 sides, then add the 2 lengths and multiply by 2 to determine the perimeter. Students will then use square tiles to cover the image to determine the area.
Instructional Tasks
Instructional Task 1
Find the whole number length and whole number width of every rectangle with an area of 18 square feet. Record the length, width and perimeter of each rectangle in the table.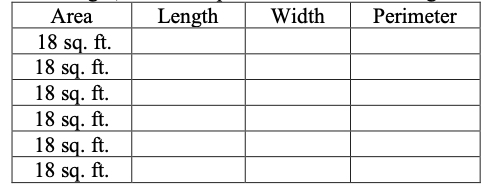
Instructional Items
Instructional Item 1
Width Perimeter Which of the following rectangles has a perimeter of 24 inches and an area of 36 square inches?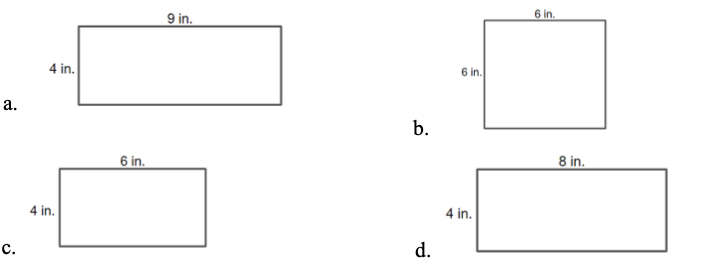
Instructional Item 2
A rectangle is 12 centimeters long and 9 centimeters wide. What is the area of the rectangle?*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
Related Access Points
Related Resources
Formative Assessment
Lesson Plans
Original Student Tutorials
STEM Lessons - Model Eliciting Activity
The students will plan a vegetable garden, deciding which kinds of vegetables to plant, how many plants of each kind will fit, and where each plant will be planted in a fixed-area garden design. Then they will revise their design based on new garden dimensions and additional plant options. Students will explore the concept of area to plan their garden and they will practice solving 1 and 2-step real-world problems using the four operations to develop their ideas.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom.
In this model eliciting activity students use data about the temperature and water requirements of plants to figure out when the plants should be planted. They also use data such as space requirements and time until harvest to make judgments about which plants would best suit the needs of students planning a school garden in Florida.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx
MFAS Formative Assessments
Students are asked to find the areas of two rectangular figures and are observed to determine if they use multiplication.
Original Student Tutorials Mathematics - Grades K-5
Explore the relationships between tiling an area, multiplication arrays and calculating area using a formula in this interactive tutorial.
Use visuals and formulas to find the perimeter and help Penelope as she creates a rectangular herb garden. Find the perimeter of rectangles using visuals and formulas in this student tutorial.
Plan some gardens by applying what you learn about perimeter in this interactive tutorial.
Student Resources
Original Student Tutorials
Use visuals and formulas to find the perimeter and help Penelope as she creates a rectangular herb garden. Find the perimeter of rectangles using visuals and formulas in this student tutorial.
Type: Original Student Tutorial
Plan some gardens by applying what you learn about perimeter in this interactive tutorial.
Type: Original Student Tutorial
Explore the relationships between tiling an area, multiplication arrays and calculating area using a formula in this interactive tutorial.
Type: Original Student Tutorial