Examples
Given the following equations, 8=8, 9-1=7, 5+2=2+5 and 1=9-8, 9-1=7 can be determined to be false.Clarifications
Clarification 1: Instruction focuses on understanding of the equal sign.Clarification 2: Problem types are limited to an equation with no more than four terms. The sum or difference can be on either side of the equal sign.
Clarification 3: Addition and subtraction are limited to sums within 20 and related subtraction facts.
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Equal Sign
- Equation
- Expression
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to understand that the equal sign means “the same as.” In Kindergarten, students used objects or drawings to explain why addition or subtraction equations are true or false.- Instruction should include a variety of problem types where the sum or difference can be on either side of the equal sign. adding 2 and 4.
- Instruction may include the use of a balance with cubes to help students understand that the equal sign means the same as (MTR.2.1, MTR.6.1).
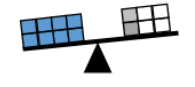
- For example, 8 = 3 + 5 is true because 8 is the result of adding 5 and 3.
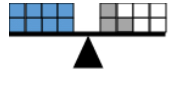
- For example, 8 = 2 + 4 is false because 8 is more than 6, which is the result of adding 2 and 4.
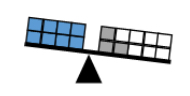
- For example, 8 = 3 + 7 is false because 8 is less than 10, which is the result of adding 3 and 7.
Common Misconceptions or Errors
- Students may not understand that the equal sign means “the same as,” since they may think the equal sign signals that the answer comes at the end. In these cases it can be beneficial to use a scale where students can complete problems to discover if in fact they are equal.
Strategies to Support Tiered Instruction
- Teacher provides number cards to build balanced equations.
- For example, using two sets of number cards 0 – 9, students build equations with two single digit addends on both sides.
- Alternatively, the teacher provides two of the missing addends and allows students to make the equation true using their number cards.

- Instruction provides opportunities to use a number balance to support understanding of the equal sign.
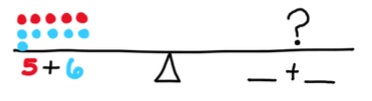
- For example, students build the expression 5 + 6 on one side of the balance and are asked to build an expression of equal magnitude of the other side. Students may choose to use a 9 and a 2, an 8 and a 3, or a 7 and a 4. Since students cannot use an 11 and must use two separate numbers instead, they are dispelling the misconception that the equal sign means “the answer is.”
Instructional Tasks
Instructional Task 1 (MTR.3.1)
Lee had 14 building blocks. He then shared 6 of his blocks with his friend Remi. Create a true statement to show how many building blocks Lee has left.
Instructional Task 2 (MTR.4.1)
Instructional Items
Instructional Item 1
Tiffany says that 9 = 8 + 1 is a true statement. Paulie says it is a false statement. Who do you agree with Tiffany or Paulie? Why?
Instructional Item 2
What does the equal sign in 11 = 10 + 1 mean?
Instructional Item 3
Which of the following statements are true?a. 17 = 18 − 1b. 16 = 16 + 1c. 14 − 6 = 8d. 12 = 12e. 2 + 8 = 11
Instructional Item 4
Create a true statement where 19 is the sum.Instructional Item 5
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
Related Access Points
Related Resources
Formative Assessments
Lesson Plans
Original Student Tutorial
Perspectives Video: Teaching Idea
Problem-Solving Tasks
Tutorial
MFAS Formative Assessments
Students are given sets of equations and asked to circle the equations that are true.
Students are given a set of equations and asked to circle the equations that are true.
Students examine four equations and state if they are true or not true. Students must also justify their reasoning.
Original Student Tutorials Mathematics - Grades K-5
Learn how to tell whether an equation is true or false based on what you know about the equal sign as you complete this interactive tutorial.
Student Resources
Original Student Tutorial
Learn how to tell whether an equation is true or false based on what you know about the equal sign as you complete this interactive tutorial.
Type: Original Student Tutorial
Problem-Solving Tasks
The purpose of this instructional task is for students to help students understand the meaning of the equal sign and to use it appropriately. The idea is that students should be comparing the number of circles in each of the rectangles and to write an equation that reflects the fact there are an equal number in each of the boxes (when this is the case).
Type: Problem-Solving Task
The purpose of this task is to help broaden and deepen students' understanding of the equals sign and equality. This task helps students attend to precision by helping them explicitly attend to the meaning of mathematical notation and carefully analyze whether it is being used correctly.
Type: Problem-Solving Task
Tutorial
In this tutorial, you will learn more about what the equals sign means and how to balance equations.
Type: Tutorial
Parent Resources
Problem-Solving Tasks
The purpose of this instructional task is for students to help students understand the meaning of the equal sign and to use it appropriately. The idea is that students should be comparing the number of circles in each of the rectangles and to write an equation that reflects the fact there are an equal number in each of the boxes (when this is the case).
Type: Problem-Solving Task
In all versions, students must engage basic addition and subtraction facts. In the memory version, after a student has turned over one card, in order to know whether there is a match using cards they've seen, they need to to solve equations of the form ?+b=c, b+?=c, ?-b=c, and b-?=c.
Type: Problem-Solving Task
The purpose of this task is to help broaden and deepen students' understanding of the equals sign and equality. This task helps students attend to precision by helping them explicitly attend to the meaning of mathematical notation and carefully analyze whether it is being used correctly.
Type: Problem-Solving Task
The act of trying to find equal lengths with the rods helps students develop a physical understanding for the meaning of equality. Students are more likely to generate and understand complex equalities than they would be able to do only abstractly.
Type: Problem-Solving Task