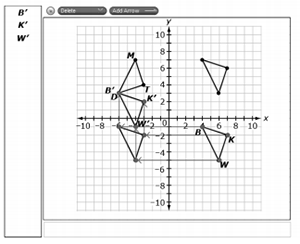
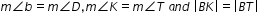Sample Test Item Preview

loading spinner
Export Print
General Information
Related Benchmark: MAFS.912.G-CO.2.8
Reporting Category: Geometry: Congruence
Type: : Multiple Types
Difficulty: N/A
Question:

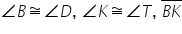
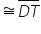
Triangles BKW and DMT are shown where angle B approximately equal to angle D comma space angle K approximately equal to angle T comma space stack B K with bar on topapproximately equal to stack D T with bar on top

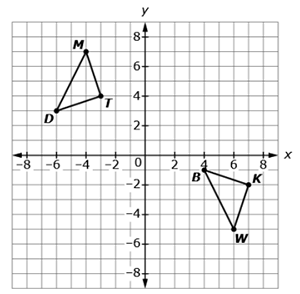
This question has three parts.

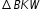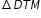Rashhaad performs a sequence of transformations on begin mathsize 12px style increment B K W end style to map it to begin mathsize 12px style increment D T M end style.

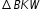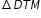Part A. Which sequence of transformations could be used to map begin mathsize 12px style increment B K W end style to begin mathsize 12px style increment D T M end style?

Part B. The coordinate grid below shows three triangles that could be an intermediate step of Rashaad's sequence of transformations.

Step 1: Use the Add Arrow tool to map the vertices of 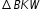begin mathsize 12px style increment B K W end style to show the translation (s) chosen in part A.

Step 2: Then, label the transformed triangle by dragging B',K', and W' to the correct vertex.

Part C.

Rashaad wants to justify that 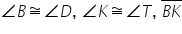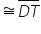angle B approximately equal to angle D comma space angle K approximately equal to angle T comma space stack B K with bar on topapproximately equal to stack D T with bar on top are sufficient to show that the triangles are congruent.

Select words, phrases or equations to complete Rashaad's justification.

Answer Options:

Part A.

A. a translation of up 8 and a reflection across the y-axis.

B. a translation of left 10, then a reflection across the x-axis.

C. a translation of left 10 and up 4, then a refection across the line y =3.

D. a translation of up 8 and a reflection across the line that passes through the origin and B'.

Possible Answer:

Part A.

C.

Part B.

Part C.

By translating 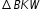begin mathsize 12px style increment B K W end style so that B maps to B', then B' coincides with D. The outcome of reflecting 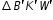begin mathsize 12px style increment B apostrophe K apostrophe W apostrophe end style is that K' coincides with T, and W' coincides with M. Because the definition of congruence in terms of rigid motions preserved distances and angles, then triangle BKW is congruent to triangle DTM. Therefore begin mathsize 12px style m angle b equals m angle D comma m angle K equals m angle T space a n d space open vertical bar B K close vertical bar equals open vertical bar B T close vertical bar end style