MA.912.AR.1.2
Examples
Algebra 1 Example: The Ideal Gas Law PV = nRT can be rearranged as  to isolate temperature as the quantity of interest.
to isolate temperature as the quantity of interest.
Example: Given the Compound Interest formula 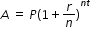 , solve for P.
, solve for P.
Mathematics for Data and Financial Literacy Honors Example: Given the Compound Interest formula 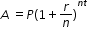 , solve for t.
, solve for t.
Clarifications
Clarification 1: Instruction includes using formulas for temperature, perimeter, area and volume; using equations for linear (standard, slope-intercept and point-slope forms) and quadratic (standard, factored and vertex forms) functions.
Clarification 2: Within the Mathematics for Data and Financial Literacy course, problem types focus on money and business.
Alternate version of this benchmark for students with significant cognitive disabilities.
Connecting Benchmarks/Horizontal Alignment
- MA.912.NSO.1.2
- MA.912.AR.2.2
- MA.912.AR.2.5
- MA.912.AR.2.6
- MA.912.AR.3.1
- MA.912.AR.3.6
- MA.912.AR.3.7
- MA.912.AR.3.8
- MA.912.AR.4.1
- MA.912.AR.5.3
- MA.912.AR.5.6
- MA.912.FL.3.2
Terms from the K-12 Glossary
- Equation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students isolated variables in one-variable linear equations and one-variable quadratic equations in the form 2 = and 3 = . In Algebra I, students isolate a variable or quantity of interest in equations and formulas. Equations and variables will focus on linear, absolute value and quadratic in Algebra I. In later courses, students will highlight a variable or quantity of interest for other types of equations and formulas, including exponential, logarithmic and trigonometric.- Instruction includes making connections to inverse arithmetic operations (refer to Appendix D) and solving one-variable equations.
- Instruction includes justifying each step while rearranging an equation or formula.
- For example, when rearranging = (1 + )
n t P
- For example, when rearranging = (1 + )
Common Misconceptions or Errors
- Students may not have mastered the inverse arithmetic operations.
- Students may be frustrated because they are not arriving at a numerical value as their solution. Remind students that they are rearranging variables that can be later evaluated to a numerical value.
- Having multiple variables and no values may confuse students and make it difficult for them to see the connections between rearranging a formula and solving a one-variable equation.
Strategies to Support Tiered Instruction
- Instruction includes doing a side-by-side comparison of solving a multistep equation
with rearranging equations and formulas. The teacher should allow students time to
understand that the steps in solving both equations are the same.
- For example, solve both equations and note the similarities in solving both types
of equations.
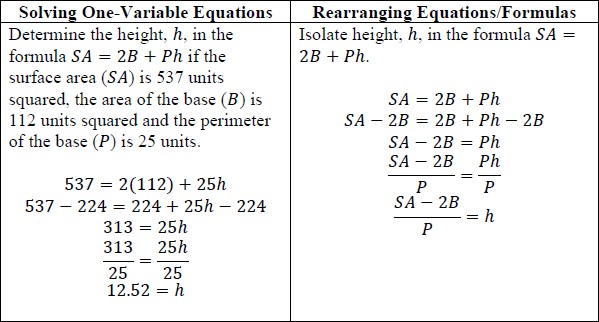
- For example, solve both equations and note the similarities in solving both types
of equations.
- Teacher provides a chart for students to use as a study guide or to copy in their
interactive notebook.
- For example, inverse operations chart below.
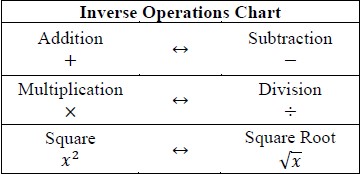
- For example, inverse operations chart below.
Instructional Tasks
Instructional Task 1 (MTR.4.1, MTR.5.1)
- Part A. Given the equation
a 2 + x b + x = 0, solve for c . x - Part B. Share your strategy with a partner. What do you notice about the new equation(s)?
Instructional Task 2 (MTR.4.1, MTR.5.1)
- Part A. Given the equation
A + x B = y , solve for C . B - Part B. Given the equation 7
− 6 x = 24, determine the y - and x -intercepts. y - Part C. What do you notice between Part A and Part B?
Instructional Items
Instructional Item 1
- Solve for
in the equation 3 x + x = 5 y − x x . y
Instructional Item 2
- The formula
= d relating to the translational of motion, where d represents distance,
0 represents initial velocity, v t represents final velocity, and v represents time. Rearrange the formula to isolate final velocity. t
Instructional Item 3
- The area
of a sector of a circle with radius A and angle-measure r (in degrees) is given by S solve for the radius
. r
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Algebraic Reasoning
Standard: Interpret and rewrite algebraic expressions and equations in equivalent forms.
Date Adopted or Revised: 08/20
Status: State Board Approved
This benchmark is part of these courses.
