General Information
Subject Area: X-Mathematics (former standards - 2008)
Grade: 8
Body of Knowledge: Geometry
Idea: Level 3: Strategic Thinking & Complex Reasoning
Big Idea: BIG IDEA 2 - Analyze two- and three-dimensional figures by using distance and angle.
Date Adopted or Revised: 09/07
Content Complexity Rating:
Level 3: Strategic Thinking & Complex Reasoning
-
More Information
Date of Last Rating: 06/07
Status: State Board Approved - Archived
Assessed: Yes
Test Item Specifications
N/A
Clarification :
Students will apply geometric properties related to similar triangles.
Students will apply geometric properties related to similar triangles.
Content Limits :
Items will not require applying the Pythagorean theorem.
Items will not require applying the Pythagorean theorem.
Stimulus Attributes :
Items may present similar triangles on the coordinate plane.
Items should be set in either a real-world or mathematical context.
Graphics should be used in most of these items, as appropriate.
Items may present similar triangles on the coordinate plane.
Items should be set in either a real-world or mathematical context.
Graphics should be used in most of these items, as appropriate.
Sample Test Items (2)
| Test Item # | Question | Difficulty | Type |
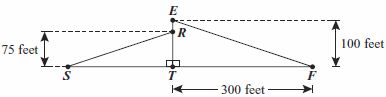
| Sample Item 1 | Two flying squirrels glided from two different points on the same tree, represented by TE in the diagram below. One squirrel glided from a height of 75 feet and the other from a height of 100 feet. Their gliding paths are represented by RS and EF in the triangles shown.
If ΔRST is similar to ΔEFT, what is the length, in feet, of ST? |
N/A | MC: Multiple Choice |
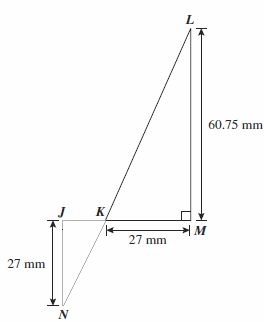
| Sample Item 2 | In the figure below, ΔJKN and ΔMKL are similar triangles.
What is the length of JM, in millimeters? |
N/A | GR: Gridded-Response |