Standard #: MA.7.G.2.1 (Archived Standard)


This document was generated on CPALMS - www.cpalms.org



Justify and apply formulas for surface area and volume of pyramids, prisms, cylinders, and cones.


Remarks


Students should be limited to prisms, pyramids and cylinders when calculating surface area, and prisms, pyramids, cylinders and cones when calculating volume.

General Information

Subject Area: X-Mathematics (former standards - 2008)
Grade: 7
Body of Knowledge: Geometry
Big Idea: BIG IDEA 2 - Develop an understanding of and use formulas to determine surface areas and volumes of three-dimensional shapes.
Date Adopted or Revised: 09/07
Content Complexity Rating: Level 2: Basic Application of Skills & Concepts - More Information
Date of Last Rating: 06/07
Status: State Board Approved - Archived
Assessed: Yes

Test Item Specifications

    Item Type(s): This benchmark may be assessed using: MC , GR item(s)
    N/A

    Clarification :
    Students will analyze a situation to justify a strategy for calculating surface area and/or volume. 

    Students will apply formulas to solve problems related to surface area of right-rectangular prisms, nonoblique triangular prisms, right-square pyramids, and right circular cylinders. 

    Students will apply formulas to solve problems related to volume of right-rectangular prisms, right triangular prisms, right-square pyramids, right-circular cylinders, and cones. 

    Students will determine one or two dimension(s) of a threedimensional figure, given its volume or surface area and the other dimensions.

    Content Limits :
    Dimensions of given figures will be whole numbers.

    Problems related to surface area will not include cones, but problems related to volume can include cones.

    In calculating surface area and volume of simple shapes, dimensions of given figures will be whole numbers.
    Stimulus Attributes :
    Items should be set in a real-world or mathematical context.

    Graphics should be used in most of these items, as appropriate.


Sample Test Items (2)

Test Item # Question Difficulty Type
Sample Item 1 Jonah is calculating the volume of a right circular cylinder. Which of the following is a correct method for calculating the volume of a cylinder? N/A MC: Multiple Choice
Sample Item 2 Maura made a wood frame and covered it with transparent red plastic wrap to create a triangular prism, as shown below.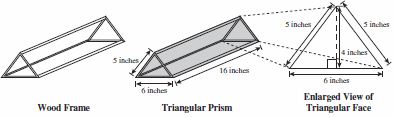

Triangular Prism

What is the total surface area, in square inches, of the prism? 		N/A GR: Gridded-Response


Related Resources

Lesson Plans

Name Description
Wrapping Up Geometry (Lesson 2 of 2)

This lesson is 2 of 2 and is primarily formative in nature, but includes a summative assessment for students to take during the following class period. 

During the lesson, students will be reviewing for their assessment on the surface area formula for a right rectangular prism. 

 

Wallpaper Woes Money Math: Lessons for Life

Students hear a story about a middle-school student who wants to redecorate his bedroom. They measure the classroom wall dimensions, draw a scale model, and incorporate measurements for windows and doors to determine the area that could be covered by wallpaper. Students then hear more about the student's redecorating adventure and learn about expenses, budget constraints, and tradeoffs.

Cylinder Volume Lesson Plan

Using volume in the real world

All wrapped up in surface area fun!

This lesson allows a hands-on approach for students to use real-life problem-solving. Students will apply their measurement skills to the concept of surface area. This lesson provides opportunities for students to work cooperatively with others as a team.

Teaching Ideas

Name Description
Modeling: Making Matchsticks This lesson unit is intended to help you assess how well students are able to:
  • Interpret a situation and represent the variables mathematically.
  • Select appropriate mathematical methods.
  • Interpret and evaluate the data generated.
  • Communicate their reasoning clearly.
The context is estimating how many matchsticks (rectangular prisms) can be made from this tree (conic).
Packing For A L-o-o-o-ng Trip To Mars In this engineering task, students will apply concepts of volume to decide what they will need to take on a 2-1/2 year journey to Mars. Then plan how to fit everything into a 1-cubic-meter box, using only a measuring tape, pencil and paper, and math.

Unit/Lesson Sequence

Name Description
Three Dimensional Shapes

In this interactive, self-guided unit on 3-dimensional shape, students (and teachers) explore 3-dimensional shapes, determine surface area and volume, derive Euler's formula, and investigate Platonic solids. Interactive quizzes and animations are included throughout, including a 15 question quiz for student completion.

Printed On:4/26/2025 8:10:50 AM
Print Page | Close this window