General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
Items may include vertical, horizontal, or other cross-sections.
Items may include more than one three-dimensional shape.
Neutral
Students will identify the shape of a two-dimensional cross-section of
a three-dimensional object.
Students will identify a three-dimensional object generated by a
rotation of a two-dimensional object
Items may be set in a real-world or mathematical context.
A verbal description of a cross-section or a three-dimensional shape
may be used.
Items may require the student to draw a line that shows the location
of a cross-section.
Sample Test Items (1)
| Test Item # | Question | Difficulty | Type |
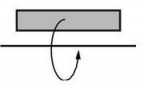
| Sample Item 1 | A rectangle and a horizontal line segment are shown.
What is the resulting object when the rectangle is rotated about the horizontal line segment? |
N/A | MC: Multiple Choice |
Related Courses
| Course Number1111 | Course Title222 |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206300: | Informal Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 1206310: | Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206320: | Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912060: | Access Informal Geometry (Specifically in versions: 2014 - 2015 (course terminated)) |
| 7912070: | Access Mathematics for Liberal Arts (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 - 2023, 2023 and beyond (current)) |
| 1206315: | Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 0102340: | Art Collaboration: Designing Solutions for Art, Work, and Life Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1207300: | Liberal Arts Mathematics 1 (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7912065: | Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current)) |
Related Resources
Formative Assessments
| Name | Description |
| Inside the Box | Students are asked to identify and draw cross sections of a rectangular prism and to describe their dimensions. |
| Slice of a Cone | Students are asked to sketch, describe, and compare three horizontal cross sections of a cone. |
| Slice It | Students are asked to identify and describe two-dimensional cross sections of three-dimensional solids. |
| 2D Rotations of Triangles | Students are given the coordinates of the vertices of a right triangle and asked to describe the solid formed by rotating the triangle about a given axis. |
| Working Backwards – 2D Rotations | Students are given a solid and asked to determine the two-dimensional shape that will create the solid when rotated about the y-axis. |
| 2D Rotations of Rectangles | Students are given the coordinates of the vertices of a rectangle and asked to describe the solid formed by rotating the rectangle about a given axis. |
Lesson Plans
| Name | Description |
| 2D Representations of 3D Objects | This lesson is intended to help you assess how well students are able to visualize two-dimensional cross-sections of representations of three-dimensional objects. In particular, the lesson will help you identify and help students who have difficulties recognizing and drawing two-dimensional cross-sections at different points along a plane of a representation of a three-dimensional object. |
| Modeling: Rolling Cups | This lesson unit is intended to help you assess how well students are able to choose appropriate mathematics to solve a non-routine problem, generate useful data by systematically controlling variables and develop experimental and analytical models of a physical situation.
|
| Representing and Combining Transformations | This lesson unit is intended to help you assess how well students are able to recognize and visualize transformations of 2D shapes, translate, reflect and rotate shapes, and combine these transformations. It also aims to encourage discussion on some common misconceptions about transformations. |
Original Student Tutorial
| Name | Description |
| Ninja Nancy Slices | Learn how to determine the shape of a cross-section created by the intersection of a slicing plane with a pyramid or prism in this ninja-themed, interactive tutorial. |
Problem-Solving Tasks
| Name | Description |
| Global Positioning System II | Reflective of the modernness of the technology involved, this is a challenging geometric modeling task in which students discover from scratch the geometric principles underlying the software used by GPS systems. |
| Tennis Balls in a Can | This task is inspired by the derivation of the volume formula for the sphere. If a sphere of radius 1 is enclosed in a cylinder of radius 1 and height 2, then the volume not occupied by the sphere is equal to the volume of a "double-naped cone" with vertex at the center of the sphere and bases equal to the bases of the cylinder |
| Global Positioning System I | This question examines the algebraic equations for three different spheres. The intersections of each pair of spheres are then studied, both using the equations and thinking about the geometry of the spheres. |
Virtual Manipulatives
| Name | Description |
| 3-D Conic Section Explorer | Using this resource, students can manipulate the measurements of a 3-D hourglass figure (double-napped cone) and its intersecting plane to see how the graph of a conic section changes. Students will see the impact of changing the height and slant of the cone and the m and b values of the plane on the shape of the graph. Students can also rotate and re-size the cone and graph to view from different angles. |
| Cross Section Flyer - Shodor | With this online Java applet, students use slider bars to move a cross section of a cone, cylinder, prism, or pyramid. This activity allows students to explore conic sections and the 3-dimensional shapes from which they are derived. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet. |
| A Plethora of Polyhedra | This program allows users to explore spatial geometry in a dynamic and interactive way. The tool allows users to rotate, zoom out, zoom in, and translate a plethora of polyhedra. The program is able to compute topological and geometrical duals of each polyhedron. Geometrical operations include unfolding, plane sections, truncation, and stellation. |
Student Resources
Original Student Tutorial
| Name | Description |
| Ninja Nancy Slices: | Learn how to determine the shape of a cross-section created by the intersection of a slicing plane with a pyramid or prism in this ninja-themed, interactive tutorial. |
Problem-Solving Tasks
| Name | Description |
| Global Positioning System II: | Reflective of the modernness of the technology involved, this is a challenging geometric modeling task in which students discover from scratch the geometric principles underlying the software used by GPS systems. |
| Tennis Balls in a Can: | This task is inspired by the derivation of the volume formula for the sphere. If a sphere of radius 1 is enclosed in a cylinder of radius 1 and height 2, then the volume not occupied by the sphere is equal to the volume of a "double-naped cone" with vertex at the center of the sphere and bases equal to the bases of the cylinder |
Virtual Manipulatives
| Name | Description |
| 3-D Conic Section Explorer: | Using this resource, students can manipulate the measurements of a 3-D hourglass figure (double-napped cone) and its intersecting plane to see how the graph of a conic section changes. Students will see the impact of changing the height and slant of the cone and the m and b values of the plane on the shape of the graph. Students can also rotate and re-size the cone and graph to view from different angles. |
| Cross Section Flyer - Shodor: | With this online Java applet, students use slider bars to move a cross section of a cone, cylinder, prism, or pyramid. This activity allows students to explore conic sections and the 3-dimensional shapes from which they are derived. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet. |
| A Plethora of Polyhedra: | This program allows users to explore spatial geometry in a dynamic and interactive way. The tool allows users to rotate, zoom out, zoom in, and translate a plethora of polyhedra. The program is able to compute topological and geometrical duals of each polyhedron. Geometrical operations include unfolding, plane sections, truncation, and stellation. |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Global Positioning System II: | Reflective of the modernness of the technology involved, this is a challenging geometric modeling task in which students discover from scratch the geometric principles underlying the software used by GPS systems. |
| Tennis Balls in a Can: | This task is inspired by the derivation of the volume formula for the sphere. If a sphere of radius 1 is enclosed in a cylinder of radius 1 and height 2, then the volume not occupied by the sphere is equal to the volume of a "double-naped cone" with vertex at the center of the sphere and bases equal to the bases of the cylinder |