General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
- Computing perimeters, areas and volumes using formulas.
- Finding the relationships between perimeters, areas, and volumes of shapes after scaling.
- Computing measurements using formulas.
- Decomposing compound shapes into simpler ones.
- Using right triangles and their properties to solve real-world problems.
Items may require the student to recall the formula for the volume of
a sphere.
Items may require the student to find a dimension.
Items that involve cones, cylinders, and spheres should require the
student to do more than just find the volume.
Items may include composite figures, including three-dimensional
figures previously learned.
Items may not include oblique figures.
Items may require the student to find the volume when one or more
dimensions are changed.
Items may require the student to find a dimension when the volume
is changed.
Neutral
Students will use volume formulas for cylinders, pyramids, cones, and
spheres to solve problems
Items must be set in a real-world context.
Items may require the student to apply the basic modeling cycle
Items may require the student to use or choose the correct unit of
measure.
Items may require the student to apply the basic modeling cycle
Sample Test Items (1)
| Test Item # | Question | Difficulty | Type |
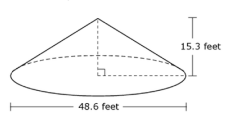
| Sample Item 1 | A phosphate is mined, it moves along a conveyor belt, falling off of the end of the belt into the shape of a right circular cone, as shown.
A shorter conveyor belt also has phosphate falling off of the end into the shape of a right circular cone. The height of the second pile of phosphate is 3.6 feet shorter than the height of the first. The volume of both piles is the same. To the nearest tenth of a foot, what is the diameter of the second pile of phosphate? |
N/A | EE: Equation Editor |
Related Courses
| Course Number1111 | Course Title222 |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206300: | Informal Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 1206310: | Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206320: | Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 2003390: | Physics 1 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912060: | Access Informal Geometry (Specifically in versions: 2014 - 2015 (course terminated)) |
| 7912070: | Access Mathematics for Liberal Arts (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 - 2023, 2023 and beyond (current)) |
| 1206315: | Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1207300: | Liberal Arts Mathematics 1 (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7912065: | Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current)) |
| 2003836: | Florida's Preinternational Baccalaureate Physics 1 (Specifically in versions: 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
Related Resources
Formative Assessments
| Name | Description |
| Snow Cones | Students are asked to solve a problem that requires calculating the volumes of a cone and a cylinder. |
| Sports Drinks | Students are asked to solve a problem that requires calculating the volume of a large cylindrical sports drink container and comparing it to the combined volumes of 24 individual containers. |
| The Great Pyramid | Students are asked to find the height of the Great Pyramid of Giza given its volume and the length of the edge of its square base. |
| Do Not Spill the Water! | Students are asked to solve a problem that requires calculating the volumes of a sphere and a cylinder. |
Lesson Plans
| Name | Description |
| Cape Florida Lighthouse: Lore and Calculations | The historic Cape Florida Lighthouse, often described as a conical tower, teems with mathematical applications. This lesson focuses on the change in volume and lateral surface area throughout its storied existence. |
| Yogurt Land Container | The student will assist Yogurt Land on choosing a new size container to offer their customers. The choice of containers are different three dimensional figures. Students will revisit the concepts of volume, surface area, and profit in order to make a decision. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Evaluating Statements About Enlargements (2D and 3D) | This lesson is intended to help you assess how well students are able to solve problems involving area and volume, and in particular, to help you identify and assist students who have difficulties with the following: |
| Volumes about Volume | This lesson explores the formulas for calculating the volume of cylinders, cones, pyramids, and spheres. |
| The Cost of Keeping Cool | Students will find the volumes of objects. After decomposing a model of a house into basic objects students will determine the cost of running the air conditioning. |
| Cylinder Volume Lesson Plan | Using volume in the real world |
| Calculating Volumes of Compound Objects | This lesson unit is intended to help you assess how well students solve problems involving measurement, and in particular, to identify and help students who have the following difficulties: |
Original Student Tutorial
| Name | Description |
| I Scream! You Scream! We All Scream for... Volume! | Learn to calculate the volume of a cone as you solve real-world problems in this ice cream-themed, interactive tutorial. |
Perspectives Video: Expert
| Name | Description |
| Carbon Foam and Geometry | <p>Carbon can take many forms, including foam! Learn more about how geometry and the Monte Carlo Method is important in understanding it.</p> |
Perspectives Video: Professional/Enthusiasts
| Name | Description |
| Volume and Surface Area of Pizza Dough | <p>Michael McKinnon of Gaines Street Pies explains how when making pizza the volume is conserved but the surface area changes.</p> |
| Mathematically Optimizing 3D Printing | <p>Did you know that altering computer code can increase 3D printing efficiency? Check it out!</p> |
| Estimating Oil Seep Production by Bubble Volume | <p>You'll need to bring your computer skills and math knowledge to estimate oil volume and rate as it seeps from the ocean floor. Dive in!</p> |
| KROS Pacific Ocean Kayak Journey: Food Storage Mass and Volume | What do you do if you don't have room for all your gear on a solo ocean trek? You're gonna need a bigger boat...or pack smarter with math. Related Resources: Download the CPALMS Perspectives video student note taking guide. |
Problem-Solving Tasks
| Name | Description |
| Doctor's Appointment | The purpose of the task is to analyze a plausible real-life scenario using a geometric model. The task requires knowledge of volume formulas for cylinders and cones, some geometric reasoning involving similar triangles, and pays attention to reasonable approximations and maintaining reasonable levels of accuracy throughout. |
| Centerpiece | The purpose of this task is to use geometric and algebraic reasoning to model a real-life scenario. In particular, students are in several places (implicitly or explicitly) to reason as to when making approximations is reasonable and when to round, when to use equalities vs. inequalities, and the choice of units to work with (e.g., mm vs. cm). |
Unit/Lesson Sequence
| Name | Description |
| Three Dimensional Shapes | In this interactive, self-guided unit on 3-dimensional shape, students (and teachers) explore 3-dimensional shapes, determine surface area and volume, derive Euler's formula, and investigate Platonic solids. Interactive quizzes and animations are included throughout, including a 15 question quiz for student completion. |
Student Resources
Original Student Tutorial
| Name | Description |
| I Scream! You Scream! We All Scream for... Volume!: | Learn to calculate the volume of a cone as you solve real-world problems in this ice cream-themed, interactive tutorial. |
Perspectives Video: Professional/Enthusiast
| Name | Description |
| Estimating Oil Seep Production by Bubble Volume: | <p>You'll need to bring your computer skills and math knowledge to estimate oil volume and rate as it seeps from the ocean floor. Dive in!</p> |
Problem-Solving Tasks
| Name | Description |
| Doctor's Appointment: | The purpose of the task is to analyze a plausible real-life scenario using a geometric model. The task requires knowledge of volume formulas for cylinders and cones, some geometric reasoning involving similar triangles, and pays attention to reasonable approximations and maintaining reasonable levels of accuracy throughout. |
| Centerpiece: | The purpose of this task is to use geometric and algebraic reasoning to model a real-life scenario. In particular, students are in several places (implicitly or explicitly) to reason as to when making approximations is reasonable and when to round, when to use equalities vs. inequalities, and the choice of units to work with (e.g., mm vs. cm). |
Parent Resources
Perspectives Video: Professional/Enthusiast
| Name | Description |
| Estimating Oil Seep Production by Bubble Volume: | <p>You'll need to bring your computer skills and math knowledge to estimate oil volume and rate as it seeps from the ocean floor. Dive in!</p> |
Problem-Solving Tasks
| Name | Description |
| Doctor's Appointment: | The purpose of the task is to analyze a plausible real-life scenario using a geometric model. The task requires knowledge of volume formulas for cylinders and cones, some geometric reasoning involving similar triangles, and pays attention to reasonable approximations and maintaining reasonable levels of accuracy throughout. |
| Centerpiece: | The purpose of this task is to use geometric and algebraic reasoning to model a real-life scenario. In particular, students are in several places (implicitly or explicitly) to reason as to when making approximations is reasonable and when to round, when to use equalities vs. inequalities, and the choice of units to work with (e.g., mm vs. cm). |