General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
Items should not require the student to use the distance or midpoint
formula.
Items should not require the student to write an equation of a circle.
Items may require the student to be familiar with using the algebraic
description (x,y) 
(x+a,y+b) for a translation, and
(x,y) (kx,ky) for a dilation when given the center of dilation.
Items may require the student to be familiar with the algebraic
description for a 90-degree rotation about the origin,
(x,y) (-y,x), for a 180-degree rotation about the origin,
(x,y) (-x,-y) , and for a 270-degree rotation about the origin,
(x,y) (y,-x) .
Items that use more than one transformation may
ask the student to write a series of algebraic descriptions.
Items should not use matrices to describe transformations.
Neutral
Students will use a sequence of transformations to prove that circles
are similar.
Students will use the measures of different parts of a circle to
determine similarity.
Circles should not be given in equation form.
Items may be set in a real-world or mathematical context.
Items may require the student to use or choose the correct unit of
measure
Sample Test Items (1)
| Test Item # | Question | Difficulty | Type |
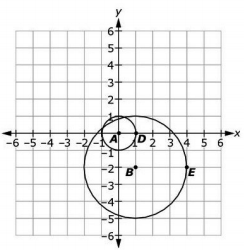
| Sample Item 1 | Circle A has a center at the origin and a point D located on the circle at (1,0). Circle B has a center at (1,-2) and a point E located on the circle at (4,-2).
Logan performs two transformations on circle A to show that circle A is similar to circle B. He first dilates the circle with the center of dilation at the origin and then translates the new circle. What are the algebraic descriptions of the two transformations? |
N/A | EE: Equation Editor |
Related Courses
| Course Number1111 | Course Title222 |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206300: | Informal Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 1206310: | Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206320: | Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912060: | Access Informal Geometry (Specifically in versions: 2014 - 2015 (course terminated)) |
| 1206315: | Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912065: | Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current)) |
Related Resources
Formative Assessments
| Name | Description |
| Similar Circles | Students are given two circles with different radii and are asked to prove that the circles are similar. |
| All Circles Are Similar | Students are given two circles with different radius lengths and are asked to prove that the circles are similar. |
Lesson Plans
| Name | Description |
| Why are Circles Similar? | Students learn how to prove that all circles are similar using the three transformations (reflection, dilation, translation) on a unique circle. The lesson takes students through multiple-step transformations to show a proof of circle similarity. A Socratic discussion is used as closure to aid in the comprehension of circle similarity. |
| Are All Circles Similar? | This lesson allows students to prove that all circles are similar using transformations. Students will need prior knowledge of similarity, transformations, and the definition of a circle. The lesson begins with a warm up regarding dilations, then poses the question: Are all circles similar? The students are guided through the proof using a translation and dilation. The teacher emphasizes the details in the proof. The lesson closes with an exit ticket. |
| Circle to Circle | Students use coordinate-based translations and dilations to prove circles are similar. |
Perspectives Video: Professional/Enthusiast
| Name | Description |
| All Circles Are Similar- Especially Circular Pizza! | What better way to demonstrate that all circles are similar then to use pizzas! Gaines Street Pies explains how all pizza pies are similar through transformations. Download the CPALMS Perspectives video student note taking guide. |