General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
Exponential functions represented in graphs or tables should be able to be written in the form a
 + k.
+ k. For exponential relationships, tables or graphs must contain at least one pair of consecutive values.
Neutral
Students will compare a linear function and an exponential function
given in real-world context by interpreting the functions’ graphs.
Students will compare a linear function and an exponential function
given in a real-world context through tables.
Students will compare a quadratic function and an exponential
function given in real-world context by interpreting the functions’
graphs.
Students will compare a quadratic function and an exponential
function given in a real-world context through tables
Items should give a graph or a table.
Items should be given in a real-world context.
Items must use function notation
Items may require the student to apply the basic modeling cycle.
Items may require the student to choose an appropriate level of
accuracy.
Items may require the student to choose and interpret the scale in a
graph.
Items may require the student to choose and interpret units
Sample Test Items (1)
| Test Item # | Question | Difficulty | Type |
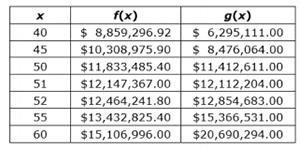
| Sample Item 1 | The function f(x) models the value of goods that are imported into the United States, where x is the number of years since 1990. The function g(x) models the value of goods that are exported from the United States.
If f(x) and g(x) continue to model the importing and exporting of goods, then sometime in 2041, which is 51 years after 1990, f(x)=g(x). Determine which function is exponential. Use the table of values to justify your answer. Type your answer in the space provided. Be sure to include your function choice. |
N/A | OR: Open Response |
Related Courses
Related Resources
Formative Assessments
| Name | Description |
| Compare Quadratic and Exponential Functions | Students are asked to compare a quadratic and an exponential function in context. |
| Compare Linear and Exponential Functions | Students are asked to compare a linear function and an exponential function in context. |
Lesson Plans
| Name | Description |
| Modeling: Having Kittens | This lesson unit is intended to help you assess how well students are able to interpret a situation and represent the constraints and variables mathematically, select appropriate mathematical methods to use, make sensible estimates and assumptions, investigate an exponentially increasing sequence and communicate their reasoning clearly. |
| Functions and Everyday Situations | This lesson unit is intended to help you assess how well students are able to articulate verbally the relationships between variables arising in everyday contexts, translate between everyday situations and sketch graphs of relationships between variables, interpret algebraic functions in terms of the contexts in which they arise and reflect on the domains of everyday functions and in particular whether they should be discrete or continuous. |
| The Power of Exponentials, Big and Small - MIT Blossoms | Exponential growth is keenly applicable to a variety of different fields ranging from cell growth in biology, nuclear chain reactions in physics to computational complexity in computer science. In this video-based lesson, through various examples and activities, we have tried to
compare exponential growth to polynomial growth and to develop an insight about how quickly the number can grow or decay in exponentials. A basic knowledge of scientific notation, plotting graphs and finding intersection of two functions is assumed. It would be better if the students have done pre-calculus, though this is not a requirement. The lesson is about 20 minutes, interspersed with simple activities that can require up to half an hour.
The webpage for this video also includes tabs where additional resources and information can be found. These include a Teacher's Guide, a Powers of 2 table, links to other helpful lessons and resources, a transcript of the video, and even an option to download the video. |
Problem-Solving Tasks
| Name | Description |
| Population and Food Supply | In this task students use verbal descriptions to construct and compare linear and exponential functions and to find where the two functions intersect (F-LE.2, F-LE.3, A-REI.11). |
| Exponential growth versus linear growth I | The purpose of this task it to have students discover how (and how quickly) an exponentially increasing quantity eventually surpasses a linearly increasing quantity. Students' intuitions will probably have them favoring Option A for much longer than is actually the case, especially if they are new to the phenomenon of exponential growth. Teachers might use this surprise as leverage to segue into a more involved task comparing linear and exponential growth. |
| Exponential growth versus polynomial growth | This problem solving task shows that an exponential function takes larger values than a cubic polynomial function provided the input is sufficiently large. This resource also includes standards alignment commentary and annotated solutions. |
| Exponential growth versus linear growth II | This task asks students to calculate exponential functions with a base larger than one. |
Unit/Lesson Sequence
| Name | Description |
| Sample Algebra 1 Curriculum Plan Using CMAP | This sample Algebra 1 CMAP is a fully customizable resource and curriculum-planning tool that provides a framework for the Algebra 1 Course. The units and standards are customizable and the CMAP allows instructors to add lessons, worksheets, and other resources as needed. This CMAP also includes rows that automatically filter and display Math Formative Assessments System tasks, E-Learning Original Student Tutorials and Perspectives Videos that are aligned to the standards, available on CPALMS. Learn more about the sample Algebra 1 CMAP, its features and customizability by watching the following video: Using this CMAPTo view an introduction on the CMAP tool, please . To view the CMAP, click on the "Open Resource Page" button above; be sure you are logged in to your iCPALMS account. To use this CMAP, click on the "Clone" button once the CMAP opens in the "Open Resource Page." Once the CMAP is cloned, you will be able to see it as a class inside your iCPALMS My Planner (CMAPs) app. To access your My Planner App and the cloned CMAP, click on the iCPALMS tab in the top menu. All CMAP tutorials can be found within the iCPALMS Planner App or at the following URL: http://www.cpalms.org/support/tutorials_and_informational_videos.aspx |
Virtual Manipulatives
| Name | Description |
| Data Flyer | Using this virtual manipulative, students are able to graph a function and a set of ordered pairs on the same coordinate plane. The constants, coefficients, and exponents can be adjusted using slider bars, so the student can explore the affect on the graph as the function parameters are changed. Students can also examine the deviation of the data from the function. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet. |
| Equation Grapher | This interactive simulation investigates graphing linear and quadratic equations. Users are given the ability to define and change the coefficients and constants in order to observe resulting changes in the graph(s). |
Student Resources
Problem-Solving Tasks
| Name | Description |
| Population and Food Supply: | In this task students use verbal descriptions to construct and compare linear and exponential functions and to find where the two functions intersect (F-LE.2, F-LE.3, A-REI.11). |
| Exponential growth versus linear growth I: | The purpose of this task it to have students discover how (and how quickly) an exponentially increasing quantity eventually surpasses a linearly increasing quantity. Students' intuitions will probably have them favoring Option A for much longer than is actually the case, especially if they are new to the phenomenon of exponential growth. Teachers might use this surprise as leverage to segue into a more involved task comparing linear and exponential growth. |
| Exponential growth versus polynomial growth: | This problem solving task shows that an exponential function takes larger values than a cubic polynomial function provided the input is sufficiently large. This resource also includes standards alignment commentary and annotated solutions. |
| Exponential growth versus linear growth II: | This task asks students to calculate exponential functions with a base larger than one. |
Virtual Manipulatives
| Name | Description |
| Data Flyer: | Using this virtual manipulative, students are able to graph a function and a set of ordered pairs on the same coordinate plane. The constants, coefficients, and exponents can be adjusted using slider bars, so the student can explore the affect on the graph as the function parameters are changed. Students can also examine the deviation of the data from the function. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet. |
| Equation Grapher: | This interactive simulation investigates graphing linear and quadratic equations. Users are given the ability to define and change the coefficients and constants in order to observe resulting changes in the graph(s). |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Population and Food Supply: | In this task students use verbal descriptions to construct and compare linear and exponential functions and to find where the two functions intersect (F-LE.2, F-LE.3, A-REI.11). |
| Exponential growth versus linear growth I: | The purpose of this task it to have students discover how (and how quickly) an exponentially increasing quantity eventually surpasses a linearly increasing quantity. Students' intuitions will probably have them favoring Option A for much longer than is actually the case, especially if they are new to the phenomenon of exponential growth. Teachers might use this surprise as leverage to segue into a more involved task comparing linear and exponential growth. |
| Exponential growth versus polynomial growth: | This problem solving task shows that an exponential function takes larger values than a cubic polynomial function provided the input is sufficiently large. This resource also includes standards alignment commentary and annotated solutions. |
| Exponential growth versus linear growth II: | This task asks students to calculate exponential functions with a base larger than one. |