General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
MAFS.912.A-APR.2.3
MAFS.912.F-IF.3.7
For F-IF.3.7, items are limited to linear, quadratic, and exponential
functions.
polynomial’s degree is restricted to 3 or 4. The polynomial function
should not have a zero with multiplicity. The polynomial should be
given in factored form.
equation to vertex form, b/a must be an even integer.
exponential growth and decay functions and to exponential functions
with one translation. Base e should not be used.
Neutral
Students will identify zeros, extreme values, and symmetry of a
quadratic function written symbolically.
or decay by examining the base, and students will give the rate of
growth or decay.
expressions in a real-world context.
Students will write an exponential function defined by an expression
in different but equivalent forms to reveal and explain different
properties of the function, and students will determine which form of
the function is the most appropriate for interpretation for a realworld context.
Students will find the zeros of a polynomial function when the
polynomial is in factored form.
Students will create a rough graph of a polynomial function in
factored form by examining the zeros of the function.
Students will use the x-intercepts of a polynomial function and end
behavior to graph the function.
Students will identify the x- and y-intercepts and the slope of the
graph of a linear function.
Students will identify zeros, extreme values, and symmetry of the
graph of a quadratic function.
Students will identify intercepts and end behavior for an exponential
function.
Students will graph a linear function using key features.
Students will graph a quadratic function using key features.
Students will graph an exponential function using key features.
Students will identify and interpret key features of a graph within the
real-world context that the function represents.
Items may require the student to identify a correct graph.
Items may be set in a mathematical or real-world context.
For F-IF.3.8, items must use function notation.
For F-IF.3.7, items may use an equation or a function.
Items should not require the student to complete a sign chart for a
polynomial.
For F-IF.3.7, items may require the student to apply the basic
modeling cycle.
Items may require the student to choose an appropriate level of
accuracy.
Items may require the student to choose and interpret the scale in a
graph.
Items may require the student to choose and interpret units.
Items may require the student to provide the answer in a specific
form.
Responses with square roots should require the student to rewrite
the square root so that the radicand has no square factors.
Sample Test Items (2)
| Test Item # | Question | Difficulty | Type |
| Sample Item 1 | A bird drops a stick from the top of Miami Tower. The height of the stick after x seconds is given by f(x)=625-16x² Select all the correct interpretations of the coordinates of the point at the maximum of the function f(x). |
N/A | MS: Multiselect |
| Sample Item 2 | A bird drops a stick from the top of Miami Tower. The height of the stick after x seconds is given by f(x)= 625-16x². What is the maximum value of f(x)? |
N/A | EE: Equation Editor |
Related Courses
| Course Number1111 | Course Title222 |
| 1200310: | Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200320: | Algebra 1 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200330: | Algebra 2 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200340: | Algebra 2 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200380: | Algebra 1-B (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1207310: | Liberal Arts Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 1298310: | Advanced Topics in Mathematics (formerly 129830A) (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 1200500: | Advanced Algebra with Financial Applications (Specifically in versions: 2014 - 2015 (course terminated)) |
| 1200410: | Mathematics for College Success (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 1200700: | Mathematics for College Algebra (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7912090: | Access Algebra 1B (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 1200315: | Algebra 1 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200335: | Algebra 2 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2019 (course terminated)) |
| 1200385: | Algebra 1-B for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1201315: | Analysis of Functions Honors (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7912075: | Access Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912095: | Access Algebra 2 (Specifically in versions: 2016 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 1200387: | Mathematics for Data and Financial Literacy (Specifically in versions: 2016 and beyond (current)) |
Related Resources
Formative Assessments
| Name | Description |
| Exponential Functions - 2 | Students are asked to identify the percent rate of change of a given exponential function. |
| Exponential Functions - 1 | Students are asked to identify the percent rate of change of a given exponential function. |
| A Home for Fido | Students are asked to rewrite a quadratic function in an equivalent form by completing the square and to use this form to identify the vertex of the graph and explain its meaning in context. |
| Launch From a Hill | Students are asked to factor and find the zeros of a polynomial function given in context. |
Lesson Plans
| Name | Description |
| The Towers of Hanoi: Experiential Recursive Thinking |
|
| Functions and Everyday Situations | This lesson unit is intended to help you assess how well students are able to articulate verbally the relationships between variables arising in everyday contexts, translate between everyday situations and sketch graphs of relationships between variables, interpret algebraic functions in terms of the contexts in which they arise and reflect on the domains of everyday functions and in particular whether they should be discrete or continuous. |
| Forming Quadratics | This lesson unit is intended to help you assess how well students are able to understand what the different algebraic forms of a quadratic function reveal about the properties of its graphical representation. In particular, the lesson will help you identify and help students who have the following difficulties in understanding how the factored form of the function can identify a graph's roots, how the completed square form of the function can identify a graph's maximum or minimum point, and how the standard form of the function can identify a graph's intercept. |
| Exponential Graphing Using Technology | This lesson is teacher/student directed for discovering and translating exponential functions using a graphing app. The lesson focuses on the translations from a parent graph and how changing the coefficient, base and exponent values relate to the transformation. |
Perspectives Video: Expert
| Name | Description |
| Using Mathematics to Optimize Wing Design | Nick Moore discusses his research behind optimizing wing design using inspiration from animals and how they swim and fly. Download the CPALMS Perspectives video student note taking guide. |
Problem-Solving Tasks
| Name | Description |
| Which Function? | The task addresses knowledge related to interpreting forms of functions derived by factoring or completing the square. It requires students to pay special attention to the information provided by the way the equation is represented as well as the sign of the leading coefficient, which is not written out explicitly, and then to connect this information to the important features of the graph. |
| Springboard Dive | The problem presents a context where a quadratic function arises. Careful analysis, including graphing of the function, is closely related to the context. The student will gain valuable experience applying the quadratic formula and the exercise also gives a possible implementation of completing the square. |
Tutorial
| Name | Description |
| Power of a Power Property | This tutorial demonstrates how to use the power of a power property with both numerals and variables. |
Unit/Lesson Sequence
| Name | Description |
| Sample Algebra 1 Curriculum Plan Using CMAP | This sample Algebra 1 CMAP is a fully customizable resource and curriculum-planning tool that provides a framework for the Algebra 1 Course. The units and standards are customizable and the CMAP allows instructors to add lessons, worksheets, and other resources as needed. This CMAP also includes rows that automatically filter and display Math Formative Assessments System tasks, E-Learning Original Student Tutorials and Perspectives Videos that are aligned to the standards, available on CPALMS. Learn more about the sample Algebra 1 CMAP, its features and customizability by watching the following video: Using this CMAPTo view an introduction on the CMAP tool, please . To view the CMAP, click on the "Open Resource Page" button above; be sure you are logged in to your iCPALMS account. To use this CMAP, click on the "Clone" button once the CMAP opens in the "Open Resource Page." Once the CMAP is cloned, you will be able to see it as a class inside your iCPALMS My Planner (CMAPs) app. To access your My Planner App and the cloned CMAP, click on the iCPALMS tab in the top menu. All CMAP tutorials can be found within the iCPALMS Planner App or at the following URL: http://www.cpalms.org/support/tutorials_and_informational_videos.aspx |
Video/Audio/Animations
| Name | Description |
| Solving Quadratic Equations using Square Roots | This video will demonstrate how to solve a quadratic equation using square roots. |
| Quadratic Functions 2 | This video gives a more in-depth look at graphing quadratic functions than previously offered in Quadratic Functions 1. |
Worksheet
| Name | Description |
| Quadratic Functions | This worksheet gives students one place to show all transformations (reflections, vertical stretches/compressions, and translations) for the quadratic function. The worksheet also has a place for domain and range for each transformation. |
Student Resources
Problem-Solving Tasks
| Name | Description |
| Which Function?: | The task addresses knowledge related to interpreting forms of functions derived by factoring or completing the square. It requires students to pay special attention to the information provided by the way the equation is represented as well as the sign of the leading coefficient, which is not written out explicitly, and then to connect this information to the important features of the graph. |
| Springboard Dive: | The problem presents a context where a quadratic function arises. Careful analysis, including graphing of the function, is closely related to the context. The student will gain valuable experience applying the quadratic formula and the exercise also gives a possible implementation of completing the square. |
Tutorial
| Name | Description |
| Power of a Power Property: | This tutorial demonstrates how to use the power of a power property with both numerals and variables. |
Video/Audio/Animations
| Name | Description |
| Solving Quadratic Equations using Square Roots: | This video will demonstrate how to solve a quadratic equation using square roots. |
| Quadratic Functions 2: | This video gives a more in-depth look at graphing quadratic functions than previously offered in Quadratic Functions 1. |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Which Function?: | The task addresses knowledge related to interpreting forms of functions derived by factoring or completing the square. It requires students to pay special attention to the information provided by the way the equation is represented as well as the sign of the leading coefficient, which is not written out explicitly, and then to connect this information to the important features of the graph. |
| Springboard Dive: | The problem presents a context where a quadratic function arises. Careful analysis, including graphing of the function, is closely related to the context. The student will gain valuable experience applying the quadratic formula and the exercise also gives a possible implementation of completing the square. |
Tutorial
| Name | Description |
| Power of a Power Property: | This tutorial demonstrates how to use the power of a power property with both numerals and variables. |

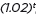 , y =
, y = 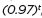 , y =
, y = 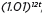 , y =
, y = 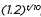 , and classify them as representing exponential growth or decay.
, and classify them as representing exponential growth or decay.