Relate the domain of a function to its graph and, where applicable, to
the quantitative relationship it describes.
For example, if the function
h(n) gives the number of person-hours it takes to assemble engines in a
factory, then the positive integers would be an appropriate domain for the
function. ★
| Course Number1111 |
Course Title222 |
| 1200310: | Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200320: | Algebra 1 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200330: | Algebra 2 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200340: | Algebra 2 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200370: | Algebra 1-A (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200380: | Algebra 1-B (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206330: | Analytic Geometry (Specifically in versions: 2014 - 2015 (course terminated)) |
| 1200500: | Advanced Algebra with Financial Applications (Specifically in versions: 2014 - 2015 (course terminated)) |
| 1200410: | Mathematics for College Success (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 1200700: | Mathematics for College Algebra (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7912070: | Access Mathematics for Liberal Arts (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 - 2023, 2023 and beyond (current)) |
| 7912080: | Access Algebra 1A (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912090: | Access Algebra 1B (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 1200315: | Algebra 1 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200335: | Algebra 2 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2019 (course terminated)) |
| 1200375: | Algebra 1-A for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200385: | Algebra 1-B for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1207300: | Liberal Arts Mathematics 1 (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7912075: | Access Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912095: | Access Algebra 2 (Specifically in versions: 2016 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 1200387: | Mathematics for Data and Financial Literacy (Specifically in versions: 2016 and beyond (current)) |
| Name |
Description |
| Compacting Cardboard | Students investigate the amount of space that could be saved by flattening cardboard boxes. The analysis includes linear graphs and regression analysis along with discussions of slope and a direct variation phenomenon. |
| Functions and Everyday Situations | This lesson unit is intended to help you assess how well students are able to articulate verbally the relationships between variables arising in everyday contexts, translate between everyday situations and sketch graphs of relationships between variables, interpret algebraic functions in terms of the contexts in which they arise and reflect on the domains of everyday functions and in particular whether they should be discrete or continuous. |
| Cup-Activity: writing equations from data | This is a great lab activity that allows students to develop a true understanding of slope as a rate of change. Students are active and involved and must use higher order thinking skills in order to answer questions. Students work through an activity, measuring heights of cups that are stacked. Students them determine a "rate of change - slope". Students are then asked to put this into slope-intercept form. The important part here is in their determining the y-intercept of the equation. Students then take this further and finally attempt to create a linear inequality to determine how many cups, stacked vertically, will fit under a table. |
| Sine Curves and Biorhythms | This is an activity in which students find their personal biorhythms using sine functions. Biorhythms are 3 cycles (physical, emotional, and intellectual) thought to affect our behavior and performance. The biorhythms have 3 different period lengths. Students need to compute the number of days they have lived to find where they are in these cycles. Students find the equations of the functions and then graph on a graphing calculator. |
| Exponential Graphing Using Technology | This lesson is teacher/student directed for discovering and translating exponential functions using a graphing app. The lesson focuses on the translations from a parent graph and how changing the coefficient, base and exponent values relate to the transformation. |
| Name |
Description |
| Average Cost | This task asks students to find the average, write an equation, find the domain, and create a graph of the cost of producing DVDs. |
| Oakland Coliseum | This deceptively simple task asks students to find the domain and range of a function from a given context. The function is linear and if simply looked at from a formulaic point of view, students might find the formula for the line and say that the domain and range are all real numbers. |
| The Canoe Trip, Variation 2 | The primary purpose of this task is to lead students to a numerical and graphical understanding of the behavior of a rational function near a vertical asymptote, in terms of the expression defining the function. |
| The Canoe Trip, Variation 1 | The purpose of this task is to give students practice constructing functions that represent a quantity of interest in a context, and then interpreting features of the function in the light of the context. It can be used as either an assessment or a teaching task. |
| Name |
Description |
| Average Cost: | This task asks students to find the average, write an equation, find the domain, and create a graph of the cost of producing DVDs. |
| Oakland Coliseum: | This deceptively simple task asks students to find the domain and range of a function from a given context. The function is linear and if simply looked at from a formulaic point of view, students might find the formula for the line and say that the domain and range are all real numbers. |
| The Canoe Trip, Variation 2: | The primary purpose of this task is to lead students to a numerical and graphical understanding of the behavior of a rational function near a vertical asymptote, in terms of the expression defining the function. |
| The Canoe Trip, Variation 1: | The purpose of this task is to give students practice constructing functions that represent a quantity of interest in a context, and then interpreting features of the function in the light of the context. It can be used as either an assessment or a teaching task. |
| Name |
Description |
| Average Cost: | This task asks students to find the average, write an equation, find the domain, and create a graph of the cost of producing DVDs. |
| Oakland Coliseum: | This deceptively simple task asks students to find the domain and range of a function from a given context. The function is linear and if simply looked at from a formulaic point of view, students might find the formula for the line and say that the domain and range are all real numbers. |
| The Canoe Trip, Variation 2: | The primary purpose of this task is to lead students to a numerical and graphical understanding of the behavior of a rational function near a vertical asymptote, in terms of the expression defining the function. |
| The Canoe Trip, Variation 1: | The purpose of this task is to give students practice constructing functions that represent a quantity of interest in a context, and then interpreting features of the function in the light of the context. It can be used as either an assessment or a teaching task. |

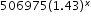 , shown on the graph.
, shown on the graph.