| Course Number1111 |
Course Title222 |
| 1200310: | Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200320: | Algebra 1 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200330: | Algebra 2 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200340: | Algebra 2 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200370: | Algebra 1-A (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200380: | Algebra 1-B (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206330: | Analytic Geometry (Specifically in versions: 2014 - 2015 (course terminated)) |
| 1200500: | Advanced Algebra with Financial Applications (Specifically in versions: 2014 - 2015 (course terminated)) |
| 1200410: | Mathematics for College Success (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 1200700: | Mathematics for College Algebra (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7912070: | Access Mathematics for Liberal Arts (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 - 2023, 2023 and beyond (current)) |
| 7912080: | Access Algebra 1A (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912090: | Access Algebra 1B (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 2000510: | Bioscience 2 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2023, 2023 - 2024, 2024 and beyond (current)) |
| 2000520: | Bioscience 3 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2023, 2023 - 2024, 2024 and beyond (current)) |
| 1200315: | Algebra 1 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200335: | Algebra 2 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2019 (course terminated)) |
| 1200375: | Algebra 1-A for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200385: | Algebra 1-B for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912100: | Fundamental Algebraic Skills (Specifically in versions: 2013 - 2015, 2015 - 2017 (course terminated)) |
| 1207300: | Liberal Arts Mathematics 1 (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7912075: | Access Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912095: | Access Algebra 2 (Specifically in versions: 2016 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 1200387: | Mathematics for Data and Financial Literacy (Specifically in versions: 2016 and beyond (current)) |
| Name |
Description |
| Quadrupling Leads to Halving | Students explore the structure of the operation s/(vn). This question provides students with an opportunity to see expressions as constructed out of a sequence of operations: first taking the square root of n, then dividing the result of that operation into s. |
| The Physics Professor | Students write explanations of the structure and function of a mathematical expression. |
| Throwing Horseshoes | Students evaluate equivalent constructions of the same expression to determine which is the most useful for determining a maximum value. |
| The Bank Account | Students explore an expression that calculates the balance of a bank account with compounding interest. |
| Radius of a Cylinder | Students are asked to interpret the effect on the value of an expression given a change in value of one of the variables. |
| Mixing Fertilizer | Students examine and answer questions related to a scenario similar to a "mixture" problem involving two different mixtures of fertilizer. In this example, students determine and then compare expressions that correspond to concentrations of various mixtures. Ultimately, students generalize the problem and verify conclusions using algebraic rather than numerical expressions. |
| Mixing Candies | Students are asked to interpret expressions and equations within the context of the amounts of caramels and truffles in a box of candy. |
| Kitchen Floor Tiles | This problem asks students to consider algebraic expressions calculating the number of floor tiles in given patterns. The purpose of this task is to give students practice in reading, analyzing, and constructing algebraic expressions, attending to the relationship between the form of an expression and the context from which it arises. The context here is intentionally thin; the point is not to provide a practical application to kitchen floors, but to give a framework that imbues the expressions with an external meaning. |
| Increasing or Decreasing? Variation 1 | Students examine variable expression that is a complex fraction with two distinct unit fractions in the denominator. Students are asked to consider how increasing one variable will affect the value of the entire expression. The variable expression is used in physics and describes the combined resistance of two resistors in parallel. |
| Delivery Trucks | This resource describes a simple scenario which can be represented by the use of variables. Students are asked to examine several variable expressions, interpret their meaning, and describe what quantities they each represent in the given context. |
| Animal Populations | In this task students interpret the relative size of variable expressions involving two variables in the context of a real world situation. All given expressions can be interpreted as quantities that one might study when looking at two animal populations. |
| Seeing Dots | The purpose of this task is to identify the structure in the two algebraic expressions by interpreting them in terms of a geometric context. Students will have likely seen this type of process before, so the principal source of challenge in this task is to encourage a multitude and variety of approaches, both in terms of the geometric argument and in terms of the algebraic manipulation. |
| Name |
Description |
| Quadrupling Leads to Halving: | Students explore the structure of the operation s/(vn). This question provides students with an opportunity to see expressions as constructed out of a sequence of operations: first taking the square root of n, then dividing the result of that operation into s. |
| Radius of a Cylinder: | Students are asked to interpret the effect on the value of an expression given a change in value of one of the variables. |
| Mixing Fertilizer: | Students examine and answer questions related to a scenario similar to a "mixture" problem involving two different mixtures of fertilizer. In this example, students determine and then compare expressions that correspond to concentrations of various mixtures. Ultimately, students generalize the problem and verify conclusions using algebraic rather than numerical expressions. |
| Mixing Candies: | Students are asked to interpret expressions and equations within the context of the amounts of caramels and truffles in a box of candy. |
| Kitchen Floor Tiles: | This problem asks students to consider algebraic expressions calculating the number of floor tiles in given patterns. The purpose of this task is to give students practice in reading, analyzing, and constructing algebraic expressions, attending to the relationship between the form of an expression and the context from which it arises. The context here is intentionally thin; the point is not to provide a practical application to kitchen floors, but to give a framework that imbues the expressions with an external meaning. |
| Delivery Trucks: | This resource describes a simple scenario which can be represented by the use of variables. Students are asked to examine several variable expressions, interpret their meaning, and describe what quantities they each represent in the given context. |
| Animal Populations: | In this task students interpret the relative size of variable expressions involving two variables in the context of a real world situation. All given expressions can be interpreted as quantities that one might study when looking at two animal populations. |
| Seeing Dots: | The purpose of this task is to identify the structure in the two algebraic expressions by interpreting them in terms of a geometric context. Students will have likely seen this type of process before, so the principal source of challenge in this task is to encourage a multitude and variety of approaches, both in terms of the geometric argument and in terms of the algebraic manipulation. |
| Name |
Description |
| Quadrupling Leads to Halving: | Students explore the structure of the operation s/(vn). This question provides students with an opportunity to see expressions as constructed out of a sequence of operations: first taking the square root of n, then dividing the result of that operation into s. |
| Radius of a Cylinder: | Students are asked to interpret the effect on the value of an expression given a change in value of one of the variables. |
| Mixing Fertilizer: | Students examine and answer questions related to a scenario similar to a "mixture" problem involving two different mixtures of fertilizer. In this example, students determine and then compare expressions that correspond to concentrations of various mixtures. Ultimately, students generalize the problem and verify conclusions using algebraic rather than numerical expressions. |
| Mixing Candies: | Students are asked to interpret expressions and equations within the context of the amounts of caramels and truffles in a box of candy. |
| Kitchen Floor Tiles: | This problem asks students to consider algebraic expressions calculating the number of floor tiles in given patterns. The purpose of this task is to give students practice in reading, analyzing, and constructing algebraic expressions, attending to the relationship between the form of an expression and the context from which it arises. The context here is intentionally thin; the point is not to provide a practical application to kitchen floors, but to give a framework that imbues the expressions with an external meaning. |
| Delivery Trucks: | This resource describes a simple scenario which can be represented by the use of variables. Students are asked to examine several variable expressions, interpret their meaning, and describe what quantities they each represent in the given context. |
| Animal Populations: | In this task students interpret the relative size of variable expressions involving two variables in the context of a real world situation. All given expressions can be interpreted as quantities that one might study when looking at two animal populations. |
| Seeing Dots: | The purpose of this task is to identify the structure in the two algebraic expressions by interpreting them in terms of a geometric context. Students will have likely seen this type of process before, so the principal source of challenge in this task is to encourage a multitude and variety of approaches, both in terms of the geometric argument and in terms of the algebraic manipulation. |

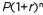 as the product of P and a factor not depending on P.
as the product of P and a factor not depending on P.