General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
Coordinate values of ?? and ?? must be integers. The number of transformations should be no more than two. In items that require the student to draw a transformed figure using a dilation or a rotation, the center of the transformation must be given.
Neutral
Allowable
Sample Test Items (3)
| Test Item # | Question | Difficulty | Type |
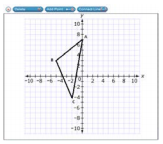
| Sample Item 1 | Triangle ABC is translated 5 units to the right to create triangle A’B’C’.
Use the Connect Line tool to draw triangle A’B’C’. |
N/A | GRID: Graphic Response Item Display |
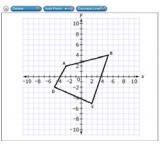
| Sample Item 2 | Quadrilateral ABCD is rotated 90° clockwise about the origin to create quadrilateral A’B’C’D’.
Use the Connect Line tool to draw quadrilateral A’B’C’D’. |
N/A | GRID: Graphic Response Item Display |
| Sample Item 3 | A pentagon is shown. The pentagon is translated 5 units to the left and then reflected over the x-axis. Use the Connect Line tool to draw the pentagon after its transformations.
|
N/A | GRID: Graphic Response Item Display |
Related Courses
| Course Number1111 | Course Title222 |
| 1205050: | M/J Accelerated Mathematics Grade 7 (Specifically in versions: 2014 - 2015, 2015 - 2020, 2020 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1205070: | M/J Grade 8 Pre-Algebra (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1204000: | M/J Foundational Skills in Mathematics 6-8 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7812030: | Access M/J Grade 8 Pre-Algebra (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912115: | Fundamental Explorations in Mathematics 2 (Specifically in versions: 2013 - 2015, 2015 - 2017 (course terminated)) |
Related Resources
Educational Software / Tool
| Name | Description |
| Transformations Using Technology | This virtual manipulative can be used to demonstrate and explore the effect of translation, rotation, and/or reflection on a variety of plane figures. A series of transformations can be explored to result in a specified final image. |
Formative Assessments
| Name | Description |
| Translation Coordinates | Students are asked to translate two-dimensional figures in the coordinate plane and identify the coordinates of the vertices of the images. |
| Rotation Coordinates | Students are asked to rotate two-dimensional figures in the coordinate plane and identify the coordinates of the vertices of the images. |
| Reflection Coordinates | Students are asked to reflect two-dimensional figures in the coordinate plane and identify the coordinates of the vertices of the images. |
| Dilation Coordinates | Students are asked to dilate two-dimensional figures in the coordinate plane and identify the coordinates of the vertices of the images. |
Lesson Plans
| Name | Description |
| Coding Geometry Challenge #10 & 11 | This set of geometry challenges focuses on scaled drawings and area as students problem solve and think as they learn to code using block coding software. Student will need to use their knowledge of the attributes of polygons and mathematical principals of geometry to accomplish the given challenges. The challenges start out fairly simple and move to more complex situations in which students can explore at their own pace or work as a team. Computer Science standards are seamlessly intertwined with the math standards while providing “Step it up!” and “Jump it up!” opportunities to increase rigor. |
| Coding Geometry Challenge #23 & 24 | This set of geometry challenges focuses on using transformations to show similarity and congruence of polygons and circles. Students problem solve and think as they learn to code using block coding software. Student will need to use their knowledge of the attributes of polygons and mathematical principals of geometry to accomplish the given challenges. The challenges start out fairly simple and move to more complex situations in which students can explore at their own pace or work as a team. Computer Science standards are seamlessly intertwined with the math standards while providing “Step it up!” and “Jump it up!” opportunities to increase rigor. |
| Slide to the Left... Slide to the Right! | Students will identify, review, and analyze transformations. They will demonstrate their understanding of transformations in the coordinate plane by creating original graphs of polygons and the images that result from specific transformations. |
| Exploring Rotations with GeoGebra | This lesson will help students understand the concept of geometric rotations. The teacher/students will use a GeoGebra applet to derive the rules for rotating a point on the coordinate plane about the origin for a 90-degree, 180-degree, and a 270-degree counterclockwise rotation. |
Problem-Solving Tasks
| Name | Description |
| Reflecting Reflections | In this resource, students experiment with the reflection of a triangle in a coordinate plane. |
| Point Reflection | The purpose of this task is for students to apply a reflection to a single point. The standard asks students to apply the effect of a single transformation on two-dimensional figures. Although this problem only applies a reflection to a single point, it has high cognitive demand if the students are prompted to supply a picture. This is because the coordinates of the point (1000,2012) are very large. If students try to plot this point and the line of reflection on the usual x-y coordinate grid, then either the graph will be too big or else the point will lie so close to the line of reflection that it is not clear whether or not it lies on this line. A good picture requires a careful choice of the appropriate region in the plane and the corresponding labels. Moreover, reflections of two-dimensional figures are found by reflecting individual points. |
| Triangle congruence with coordinates | In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking. |
Student Center Activity
| Name | Description |
| Edcite: Mathematics Grade 8 | Students can practice answering mathematics questions on a variety of topics. With an account, students can save their work and send it to their teacher when complete. |
Tutorial
| Name | Description |
| Scaling Down a Triangle by Half | This video demonstrates the effect of a dilation on the coordinates of a triangle. |
Virtual Manipulative
| Name | Description |
| Rotation of a Point | This virtual manipulative is an interactive visual presentation of the rotation of a point around the origin of the coordinate system. The original point can be dragged to different positions and the angle of rotation can be changed with a 90° increment. |
Student Resources
Educational Software / Tool
| Name | Description |
| Transformations Using Technology: | This virtual manipulative can be used to demonstrate and explore the effect of translation, rotation, and/or reflection on a variety of plane figures. A series of transformations can be explored to result in a specified final image. |
Problem-Solving Tasks
| Name | Description |
| Reflecting Reflections: | In this resource, students experiment with the reflection of a triangle in a coordinate plane. |
| Point Reflection: | The purpose of this task is for students to apply a reflection to a single point. The standard asks students to apply the effect of a single transformation on two-dimensional figures. Although this problem only applies a reflection to a single point, it has high cognitive demand if the students are prompted to supply a picture. This is because the coordinates of the point (1000,2012) are very large. If students try to plot this point and the line of reflection on the usual x-y coordinate grid, then either the graph will be too big or else the point will lie so close to the line of reflection that it is not clear whether or not it lies on this line. A good picture requires a careful choice of the appropriate region in the plane and the corresponding labels. Moreover, reflections of two-dimensional figures are found by reflecting individual points. |
| Triangle congruence with coordinates: | In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking. |
Student Center Activity
| Name | Description |
| Edcite: Mathematics Grade 8: | Students can practice answering mathematics questions on a variety of topics. With an account, students can save their work and send it to their teacher when complete. |
Tutorial
| Name | Description |
| Scaling Down a Triangle by Half: | This video demonstrates the effect of a dilation on the coordinates of a triangle. |
Virtual Manipulative
| Name | Description |
| Rotation of a Point: | This virtual manipulative is an interactive visual presentation of the rotation of a point around the origin of the coordinate system. The original point can be dragged to different positions and the angle of rotation can be changed with a 90° increment. |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Reflecting Reflections: | In this resource, students experiment with the reflection of a triangle in a coordinate plane. |
| Point Reflection: | The purpose of this task is for students to apply a reflection to a single point. The standard asks students to apply the effect of a single transformation on two-dimensional figures. Although this problem only applies a reflection to a single point, it has high cognitive demand if the students are prompted to supply a picture. This is because the coordinates of the point (1000,2012) are very large. If students try to plot this point and the line of reflection on the usual x-y coordinate grid, then either the graph will be too big or else the point will lie so close to the line of reflection that it is not clear whether or not it lies on this line. A good picture requires a careful choice of the appropriate region in the plane and the corresponding labels. Moreover, reflections of two-dimensional figures are found by reflecting individual points. |
| Triangle congruence with coordinates: | In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking. |