General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
Items should not use variables. Items should require two or more steps
Yes
Required
Sample Test Items (5)
| Test Item # | Question | Difficulty | Type |
| Sample Item 1 | Rolando is 13. In five years, his age will be How old will Marisa be in three years?
|
N/A | EE: Equation Editor |
| Sample Item 2 | A set of pencils sells for $1.75 and costs $0.40 to make. Twenty percent of the profit
(the difference between the purchase price and the amount it costs to make) from
each set of pencils goes to a school. If 500 sets are sold, what is the amount of money that will go to the school? |
N/A | EE: Equation Editor |
| Sample Item 3 | A bucket holds 243.5 ounces (oz) of water when full. The bucket loses 0.3 oz of water
per second. In how many seconds will the bucket be 40% full? |
N/A | EE: Equation Editor |
| Sample Item 4 | A plane is flying at 31,348 feet. It needs to rise to 36,000 feet in two stages. In stage 1, it rises 5% of its initial altitude of 31,348 feet. In stage 2, it rises at a rate of 140.3 feet per minute. How many minutes does it take for the plane to rise during stage 2? |
N/A | EE: Equation Editor |
| Sample Item 5 | The dimensions of a rectangular pool are 24.5 feet by 13 feet. The depth of the water is 4 feet. Each cubic foot contains 7.48 gallons of water. How many gallons of water, to the nearest tenth, are needed to fill the pool to 80% capacity? |
N/A | EE: Equation Editor |
Related Courses
| Course Number1111 | Course Title222 |
| 1205040: | M/J Grade 7 Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1205050: | M/J Accelerated Mathematics Grade 7 (Specifically in versions: 2014 - 2015, 2015 - 2020, 2020 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1204000: | M/J Foundational Skills in Mathematics 6-8 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200410: | Mathematics for College Success (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated)) |
| 7812020: | Access M/J Grade 7 Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912115: | Fundamental Explorations in Mathematics 2 (Specifically in versions: 2013 - 2015, 2015 - 2017 (course terminated)) |
Related Resources
Educational Games
| Name | Description |
| Timed Algebra Quiz | In this timed activity, students solve linear equations (one- and two-step) or quadratic equations of varying difficulty depending on the initial conditions they select. This activity allows students to practice solving equations while the activity records their score, so they can track their progress. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet. |
| Algebra Four | In this activity, two students play a simulated game of Connect Four, but in order to place a piece on the board, they must correctly solve an algebraic equation. This activity allows students to practice solving equations of varying difficulty: one-step, two-step, or quadratic equations and using the distributive property if desired. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the Java applet. |
Formative Assessments
| Name | Description |
| Using Estimation | Students are asked to assess the reasonableness of answers using estimation strategies. |
| Alexa’s Account | Students are asked to assess the reasonableness of an answer using mental computation and estimation strategies. |
| Gas Station Equations | Students are asked to solve a multi-step problem involving percent. |
| Reeling in Expressions | Students are asked to solve a multi-step problem involving rational numbers. |
| Discount and Tax | Students are asked to solve a multi-step problem involving percent. |
Lesson Plans
| Name | Description |
| Gather Data For Distribution by Programming an App | This lesson allow students to gather, calculate, and plot data using both computer code and mathematical equations. In this lesson students will create a pedometer app to demonstrate the understanding of algorithms, components (such as buttons, textboxes, sensors, etc.), and If/Then statements. This lesson uses algebraic equations and random data to access the needed components to store data in a spreadsheet. |
| Radioactive Dating: Half-Life & Geologic Time | In this Model Eliciting Activity (MEA), students must use their knowledge of radioactive dating and geologic time to select an effective elemental isotope to be used to date three rare specimens. This decision requires an understanding of the concept of a half-life and the benefits and limitations of radiometric dating. Students must complete mathematical calculations involving equations and operations with fractions and percentages. Students completing this MEA must develop two essays that respond in a professional manner to a client in the scientific industry. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| How Fast Can One Travel on a Bicycle? | Students investigate how the pedal and rear wheel gears affect the speed of a bicycle. A GeoGebra sketch is included that allows a simulation of the turning of the pedal and the rear wheel. A key goal is to provide an experience for the students to apply and integrate the key concepts in seventh-grade mathematics in a familiar context. |
| 3-D Printers: Cost Effective for the Quality? | Students will compare the cost of pre-made solar car kits to cars made from a 3-D printer. In the second part of the activity, students will research other available 3-D printers and determine what attributes are important to consider. There is also an optional solar panel car race for day 3. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Steps to Solving Equations | This lesson unit is intended to help you assess how well students are able to form and solve linear equations involving factorizing and using the distributive law. In particular, this unit aims to help you identify and assist students who have difficulties in using variables to represent quantities in a real-world or mathematical problem and solving word problems leading to equations of the form px + q = r and p(x + q) = r. |
| Percent of Change | Students will investigate percent of change in real-world situations and will differentiate between an increase or a decrease. The students will use a formula to find the percent of change. |
| In Whose Best Interest is Interest? | Students will use simple interest to explore real world examples of interest rates. Students will explore loan rates, CD rates and compare benefits of different rates versus different terms of loans. |
| It's All About Properties of Equality | Students will apply properties of equality to solve multi-step equations with one variable. Students will complete a gallery walk as formative assessment, to determine students' understanding of properties of operations and equality when applied to equations. Equations increase in difficulty as the lesson progresses. Students complete an error analysis toward the end of the lesson. This lesson includes a powerpoint presentation. |
| Pricing Twelve Days of Celebration | Students will discover how much items would cost if they were to give gifts for 12 days. They will learn how to calculate and add sales tax to find a total. |
| Travel Troubles | This activity engages the students into time scheduling, budgeting, and decision making to maximize time efficiency. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought processes. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEAs visit: https://www.cpalms.org/cpalms/mea.aspx. |
| Batteries Included | In this Model Eliciting Activity, MEA, students will evaluate batteries using empirical data and customer comments to help a Taxi Cab Service decide which battery brand to purchase. In this real-world scenario, students will communicate with the client in letter format stating their suggested ranking. They will also provide calculations and justification for each decision. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought processes. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx |
| Where in the world? | This resource provides a Model-Eliciting Activity where students will analyze a real-world scenario to solve a client's problem and provide the best possible solution based on a logically justified process. The students will consider a request from Always On Time Delivery Service to evaluate several GPS units and help them decide which unit they should purchase. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought processes. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEAs visit: https://www.cpalms.org/cpalms/mea.aspx |
| Math in Mishaps | Students will explore how percentages, proportions, and solving for unknowns are used in important jobs. This interactive activity will open their minds and address the question, "When is this ever used in real life?" |
| Which Food Should I Feed My Cat? | The students will convert fractions into decimals and multiply to determine the amount of food to feed their assigned cat. Using this amount, they will calculate (division of decimals) the number of servings and the price per serving of cat food. Students will work with three brands of food and enter the data into their charts. Finally, the students will analyze the data to determine the most affordable food. |
| Here's a tip! | Students will solve problems involving sales tax and tips; students will apply the properties of operations with numbers in decimal, percent, and fraction form. Students will convert between numbers in any form as appropriate. |
| Uncle Henry's Dilemma | Uncle Henry's Dilemma is a problem solving lesson to determine the global location for the reading of Uncle Henry's will. The students will interpret data sets which include temperature, rainfall, air pollution, travel cost, flight times and health issues to rank five global locations for Uncle Henry's relatives to travel to for the reading of his will. This is an engaging, fun-filled MEA lesson with twists and turns throughout. Students will learn how this procedure of selecting locations can be applied to everyday decisions by the government, a business, a family, or individuals. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Let's Go Shopping: Calculating Percents | In this lesson, students will participate in a simulated shopping experience where they choose items they would like to purchase from local sale advertisements. The students will be able to apply the percent formula and the percent of change formula to real world financial situations. Students will learn how to calculate percent discounts, their percent of savings, and tax. The students will analyze, compare, draw conclusions and explain in writing why specific types of discounts are the most advantageous given specific situations. |
| Understanding Decimals | These games and activities help students investigate the relationship between fractions and decimals, focusing on equivalence. |
Original Student Tutorial
| Name | Description |
| Balancing the Machine | Use models to solve balance problems on a space station in this interactive, math and science tutorial. |
Problem-Solving Tasks
| Name | Description |
| Maximizing Area: Gold Rush | Before the lesson, students attempt the Gold Rush task individually. You then look at their responses and formulate questions for students to think about as they review their work. At the start of the lesson, students reflect on their individual responses and use the questions posed to think of ways to improve their work. Next, students work collaboratively in small groups to produce, in the form of a poster, a better solution to the Gold Rush task than they did individually. In a whole-class discussion students compare and evaluate the different methods they used. Working in small groups, students analyze sample responses to the Gold Rush task, then, in a whole-class discussion, review the methods they have seen. Finally, students reflect on their work. |
| Anna in D.C. | The purpose of this task is to give students an opportunity to solve a challenging multistep percentage problem that can be approached in several different ways. Students are asked to find the cost of a meal before tax and tip when given the total cost of the meal. The task can illustrate multiple standards depending on the prior knowledge of the students and the approach used to solve the problem. |
| Discounted Books | This purpose of this task is to help students see two different ways to look at percentages both as a decrease and an increase of an original amount. In addition, students have to turn a verbal description of several operations into mathematical symbols. This requires converting simple percentages to decimals as well as identifying equivalent expressions without variables. |
| Guess My Number | This problem asks the students to represent a sequence of operations using an expression and then to write and solve simple equations. The problem is posed as a game and allows the students to visualize mathematical operations. It would make sense to actually play a similar game in pairs first and then ask the students to record the operations to figure out each other's numbers. |
| Shrinking | Students are asked to determine the change in height in inches when given a constant rate of change in centimeters. The answer is rounded to the nearest half inch. |
| Gotham City Taxis | The purpose of this task is to give students an opportunity to solve a multi-step ratio problem that can be approached in many ways. This can be done by making a table, which helps illustrate the pattern of taxi rates for different distances traveled and with a little persistence leads to a solution which uses arithmetic. It is also possible to calculate a unit rate (dollars per mile) and use this to find the distance directly without making a table. |
Tutorials
| Name | Description |
| Solving Percentage Problems with Linear Equations | Many real world problems involve involve percentages. This lecture shows how algebra is used in solving problems of percent change and profit-and-loss. |
| Age word problem | Students will learn how to set up and solve an age word problem. |
Video/Audio/Animation
| Name | Description |
| Averages | This Khan Academy video tutorial introduces averages and algebra problems involving averages. |
Student Resources
Original Student Tutorial
| Name | Description |
| Balancing the Machine: | Use models to solve balance problems on a space station in this interactive, math and science tutorial. |
Educational Games
| Name | Description |
| Timed Algebra Quiz: | In this timed activity, students solve linear equations (one- and two-step) or quadratic equations of varying difficulty depending on the initial conditions they select. This activity allows students to practice solving equations while the activity records their score, so they can track their progress. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet. |
| Algebra Four: | In this activity, two students play a simulated game of Connect Four, but in order to place a piece on the board, they must correctly solve an algebraic equation. This activity allows students to practice solving equations of varying difficulty: one-step, two-step, or quadratic equations and using the distributive property if desired. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the Java applet. |
Problem-Solving Tasks
| Name | Description |
| Anna in D.C.: | The purpose of this task is to give students an opportunity to solve a challenging multistep percentage problem that can be approached in several different ways. Students are asked to find the cost of a meal before tax and tip when given the total cost of the meal. The task can illustrate multiple standards depending on the prior knowledge of the students and the approach used to solve the problem. |
| Discounted Books: | This purpose of this task is to help students see two different ways to look at percentages both as a decrease and an increase of an original amount. In addition, students have to turn a verbal description of several operations into mathematical symbols. This requires converting simple percentages to decimals as well as identifying equivalent expressions without variables. |
| Guess My Number: | This problem asks the students to represent a sequence of operations using an expression and then to write and solve simple equations. The problem is posed as a game and allows the students to visualize mathematical operations. It would make sense to actually play a similar game in pairs first and then ask the students to record the operations to figure out each other's numbers. |
| Shrinking: | Students are asked to determine the change in height in inches when given a constant rate of change in centimeters. The answer is rounded to the nearest half inch. |
| Gotham City Taxis: | The purpose of this task is to give students an opportunity to solve a multi-step ratio problem that can be approached in many ways. This can be done by making a table, which helps illustrate the pattern of taxi rates for different distances traveled and with a little persistence leads to a solution which uses arithmetic. It is also possible to calculate a unit rate (dollars per mile) and use this to find the distance directly without making a table. |
Tutorials
| Name | Description |
| Solving Percentage Problems with Linear Equations: | Many real world problems involve involve percentages. This lecture shows how algebra is used in solving problems of percent change and profit-and-loss. |
| Age word problem : | Students will learn how to set up and solve an age word problem. |
Video/Audio/Animation
| Name | Description |
| Averages: | This Khan Academy video tutorial introduces averages and algebra problems involving averages. |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Anna in D.C.: | The purpose of this task is to give students an opportunity to solve a challenging multistep percentage problem that can be approached in several different ways. Students are asked to find the cost of a meal before tax and tip when given the total cost of the meal. The task can illustrate multiple standards depending on the prior knowledge of the students and the approach used to solve the problem. |
| Discounted Books: | This purpose of this task is to help students see two different ways to look at percentages both as a decrease and an increase of an original amount. In addition, students have to turn a verbal description of several operations into mathematical symbols. This requires converting simple percentages to decimals as well as identifying equivalent expressions without variables. |
| Guess My Number: | This problem asks the students to represent a sequence of operations using an expression and then to write and solve simple equations. The problem is posed as a game and allows the students to visualize mathematical operations. It would make sense to actually play a similar game in pairs first and then ask the students to record the operations to figure out each other's numbers. |
| Shrinking: | Students are asked to determine the change in height in inches when given a constant rate of change in centimeters. The answer is rounded to the nearest half inch. |
| Gotham City Taxis: | The purpose of this task is to give students an opportunity to solve a multi-step ratio problem that can be approached in many ways. This can be done by making a table, which helps illustrate the pattern of taxi rates for different distances traveled and with a little persistence leads to a solution which uses arithmetic. It is also possible to calculate a unit rate (dollars per mile) and use this to find the distance directly without making a table. |
Video/Audio/Animation
| Name | Description |
| Averages: | This Khan Academy video tutorial introduces averages and algebra problems involving averages. |

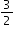 the age of his sister Marisa.
the age of his sister Marisa.