General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
- Translating between percents, decimals, and fractions.
- Representing percent increase and decrease as multiplication.
- Recognizing the relationship between increases and decreases.
The item stem must include at least one fraction. Ratios may be expressed as fractions, with “:” or with words. Units may be the same or different across the two quantities.
yes
allowable
Sample Test Items (5)
| Test Item # | Question | Difficulty | Type |
| Sample Item 1 | A recipe used 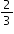 cup of sugar for every 2 teaspoons of vanilla. How much sugar
was used per teaspoon of vanilla? cup of sugar for every 2 teaspoons of vanilla. How much sugar
was used per teaspoon of vanilla?
|
N/A | MC: Multiple Choice |
| Sample Item 2 | A recipe calls for 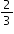 cup of sugar for every 4 teaspoons of vanilla. How much vanilla
should be used for every 1 cup of sugar? cup of sugar for every 4 teaspoons of vanilla. How much vanilla
should be used for every 1 cup of sugar?
|
N/A | MC: Multiple Choice |
| Sample Item 3 | A recipe calls for 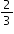 cup of sugar for every 2 teaspoons of vanilla. what is the unit
rate in cups per teaspoon? cup of sugar for every 2 teaspoons of vanilla. what is the unit
rate in cups per teaspoon? |
N/A | EE: Equation Editor |
| Sample Item 4 | A recipe calls for 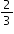 cup of sugar for every 4 teaspoons of vanilla. what is the unit
rate in teaspoons per cup? cup of sugar for every 4 teaspoons of vanilla. what is the unit
rate in teaspoons per cup? |
N/A | EE: Equation Editor |
| Sample Item 5 | A recipe calls for |
N/A | EE: Equation Editor |
Related Courses
| Course Number1111 | Course Title222 |
| 1205020: | M/J Accelerated Mathematics Grade 6 (Specifically in versions: 2014 - 2015, 2015 - 2020, 2020 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1205040: | M/J Grade 7 Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1204000: | M/J Foundational Skills in Mathematics 6-8 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7812020: | Access M/J Grade 7 Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912115: | Fundamental Explorations in Mathematics 2 (Specifically in versions: 2013 - 2015, 2015 - 2017 (course terminated)) |
Related Resources
Formative Assessments
| Name | Description |
| Unit Rate Length | Students are asked to write ratios and unit rates from fractional values. |
| Unit Rate Area | Students are asked to convert a ratio of mixed numbers to a unit rate and explain its contextual meaning. |
| Comparing Unit Rates | Students are asked to compute unit rates from values that include fractions. |
| Computing Unit Rates | Students are asked to compute and interpret unit rates in two different ways from values that include fractions and mixed numbers. |
Lesson Plans
| Name | Description |
| How Fast Can One Travel on a Bicycle? | Students investigate how the pedal and rear wheel gears affect the speed of a bicycle. A GeoGebra sketch is included that allows a simulation of the turning of the pedal and the rear wheel. A key goal is to provide an experience for the students to apply and integrate the key concepts in seventh-grade mathematics in a familiar context. |
| Bubble Burst Corporation's Chewing Gum Prototypes | In this Model Eliciting Activities, MEA, students will calculate unit rate & circumference, compare & order decimals, convert metric units, and round decimals. Bubble Burst Corporation has developed some chewing gum prototypes and has requested the students to assist in the selection of which gum prototypes will be mass produced by using both quantitative and qualitative data to rank the prototypes for Bubble Burst Corporation. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought processes. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEAs visit: https://www.cpalms.org/cpalms/mea.aspx |
| Laura’s Babysitting Job | In this 7th grade MEA Laura Banks requests a consulting firm, JJ Consulting, to help her make a decision on an employer. Students are to use the data table to calculate unit rates (nightly rate and hourly rate) and then rank her choices and write a recommendation with the procedure used to come up with the ranking. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| HOORAH!! Pizza For Lunch | The principal of Central Middle School is thinking of adding pizza to the lunch menu on Mondays and Fridays but needs help deciding the costs per slice and what students think is important about the pizza. After the students' initial decision about the pizza the principal remembers that there is a delivery charge.The students must revisit their decision and do additional calculations to see if their original process still works. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Basketball Tournament | Students at a local middle school are interested in attending a basketball tournament in Orlando. There is an entrance fee and hotel costs to consider. Students must calculate the total cost and the cost per student to attend the tournament. Each hotel has different qualities that could influence the students' choice of which hotel is best for their team. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Recognizing Proportional Relationships to Develop Sense of Scale | This 90-minute lesson (15-minute pre-lesson, 60-minute lesson and 15-minute follow up lesson or homework) asks students to analyze proportional relationships to solve real world and mathematical problems. The examples use recipes, paint, and buildings. Students begin by working individually, then in pairs or threes, and then as a whole class. Student will need calculators, large sheets of paper to make a poster and the lesson materials. |
| Increasing and Decreasing Quantities by a Percent | This lesson unit is intended to help you assess how well students are
able to interpret percent increase and decrease, and in particular, to
identify and help students who have the following difficulties:
|
| For Students by Students | Students are presented with the task of evaluating several types of fabric based on each of its characteristics. They need to analyze their current uniform needs and decide by choosing which type of fabric will best fit their uniform needs. Then they have to write a report explaining the procedure they used to analyze their choices, reasoning for their ranking and make the requested recommendations. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Let's Rate it! | The purpose of this lesson is to introduce rates of change to students, allowing them to explore how rates are formed, what rates are used for, and how rates can be used to solve real life problems. |
| Summer Road Trip | Students will go on a virtual "road trip" with a partner. Using the scale on a map, students will calculate the distance traveled, the amount of gas used, and the cost of the gas. |
| How does scale factor affect the areas and perimeters of similar figures? | In this lesson plan, students will observe and record the linear dimensions of similar figures, and then discover how the values of area and perimeter are related to the ratio of the linear dimensions of the figures. |
Perspectives Video: Expert
| Name | Description |
| Statistical Sampling Results in setting Legal Catch Rate | Fish Ecologist, Dean Grubbs, discusses how using statistical sampling can help determine legal catch rates for fish that may be endangered. Download the CPALMS Perspectives video student note taking guide. |
Perspectives Video: Professional/Enthusiasts
| Name | Description |
| Unit Rate: Spring Water Bottling | Nestle Waters discusses the importance of unit rate in the manufacturing process of bottling spring water. Download the CPALMS Perspectives video student note taking guide. |
| Unit Rate and Florida Cave Formation | How long does it take to form speleothems in the caves at Florida Caverns State Parks? Download the CPALMS Perspectives video student note taking guide. |
| Pizza Pi: Area, Circumference & Unit Rate | How many times larger is the area of a large pizza compared to a small pizza? Which pizza is the better deal? Michael McKinnon of Gaines Street Pies talks about how the area, circumference and price per square inch is different depending on the size of the pizza. Download the CPALMS Perspectives video student note taking guide. |
| Amping Up Violin Tuning with Math | Kyle Dunn, a Tallahassee-based luthier and owner of Stringfest, discusses how math is related to music. Download the CPALMS Perspectives video student note taking guide. |
| Gear Heads and Gear Ratios | <p>Have a need for speed? Get out your spreadsheet! Race car drivers use algebraic formulas and spreadsheets to optimize car performance.</p> |
Problem-Solving Tasks
| Name | Description |
| A Golden Crown? | This is a challenge problem that includes an assessment rubric. It involves working with volume, mass, and density. The setting is historical, modeling the Archimedes Golden Crown problem, when Archimedes proved that the king's crown was not pure gold. |
| Cooking with the Whole Cup | Students are asked to use proportional reasoning to answer a series of questions in the context of a recipe. |
| Molly's Run | This task asks students to solve a problem in a context involving constant speed. This task provides a transition from working with ratios involving whole numbers to ratios involving fractions. This problem can be thought of in several ways; in particular, this problem also provides an opportunity for students to work with the "How many in one group?'' interpretation of division. |
| Music Companies, Variation 1 | This problem requires a comparison of rates where one is given in terms of unit rates, and the other is not. See "Music Companies, Variation 2" for a task with a very similar setup but is much more involved and so illustrates . |
| Track Practice | This activity asks the student to use unit rate and proportional reasoning to determine which of two runners is the fastest. |
Teaching Ideas
| Name | Description |
| Scaling the Pyramids | This web page features activities that compare the Great Pyramid to such modern structures as the Statue of Liberty and the Eiffel Tower. In the first activity, students use a template to construct a scale model of the Great Pyramid. They must find the scale heights for the tallest building in their neighborhood or for their height. In the remaining activity, students are given the dimensions for two other pyramids and challenged to create models. |
| Top Speed At Sea-SeaWorld Classroom Activity | In this activity, the students will calculate the top speeds of two dolphin species (killer whales and striped dolphin) and compare them to several marine animals' speeds. |
Tutorials
| Name | Description |
| Determining Rates with Fractions | This video demonstrates finding a unit rate from a rate containing fractions. |
| Rate Problem With Fractions | Watch as we solve a rate problem finding speed in meters per second using distance (in meters) and time (in seconds). |
| Converting Speed Units | In this lesson, students will be viewing a Khan Academy video that will show how to convert ratios using speed units. |
Student Resources
Problem-Solving Tasks
| Name | Description |
| Cooking with the Whole Cup: | Students are asked to use proportional reasoning to answer a series of questions in the context of a recipe. |
| Molly's Run: | This task asks students to solve a problem in a context involving constant speed. This task provides a transition from working with ratios involving whole numbers to ratios involving fractions. This problem can be thought of in several ways; in particular, this problem also provides an opportunity for students to work with the "How many in one group?'' interpretation of division. |
| Music Companies, Variation 1: | This problem requires a comparison of rates where one is given in terms of unit rates, and the other is not. See "Music Companies, Variation 2" for a task with a very similar setup but is much more involved and so illustrates . |
| Track Practice: | This activity asks the student to use unit rate and proportional reasoning to determine which of two runners is the fastest. |
Tutorials
| Name | Description |
| Determining Rates with Fractions: | This video demonstrates finding a unit rate from a rate containing fractions. |
| Rate Problem With Fractions: | Watch as we solve a rate problem finding speed in meters per second using distance (in meters) and time (in seconds). |
| Converting Speed Units: | In this lesson, students will be viewing a Khan Academy video that will show how to convert ratios using speed units. |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Cooking with the Whole Cup: | Students are asked to use proportional reasoning to answer a series of questions in the context of a recipe. |
| Molly's Run: | This task asks students to solve a problem in a context involving constant speed. This task provides a transition from working with ratios involving whole numbers to ratios involving fractions. This problem can be thought of in several ways; in particular, this problem also provides an opportunity for students to work with the "How many in one group?'' interpretation of division. |
| Music Companies, Variation 1: | This problem requires a comparison of rates where one is given in terms of unit rates, and the other is not. See "Music Companies, Variation 2" for a task with a very similar setup but is much more involved and so illustrates . |
| Track Practice: | This activity asks the student to use unit rate and proportional reasoning to determine which of two runners is the fastest. |

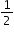 teaspoon of vanilla. What is the unit rate of cups per teaspoon?
teaspoon of vanilla. What is the unit rate of cups per teaspoon?