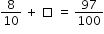General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
Denominators must be either 10 or 100. Decimal notation may not be assessed at this standard.
No
Allowable
Sample Test Items (4)
| Test Item # | Question | Difficulty | Type |
| Sample Item 1 | Create a fraction with a denominator of 100 that is equivalent to |
N/A | EE: Equation Editor |
| Sample Item 2 | Which fraction is equivalent to |
N/A | MC: Multiple Choice |
| Sample Item 3 | An equation is shown.
What is the missing fraction? |
N/A | EE: Equation Editor |
| Sample Item 4 | Melvin mows a lawn. The fraction of the lawn that Melvin has mowed so far is represented by the shaded model shown.
Melvin will mow What fraction of the lawn will Melvin have mowed when he takes his first break? |
N/A | EE: Equation Editor |
Related Courses
| Course Number1111 | Course Title222 |
| 5012060: | Grade Four Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7712050: | Access Mathematics Grade 4 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current)) |
| 5020110: | STEM Lab Grade 4 (Specifically in versions: 2016 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 5012065: | Grade 4 Accelerated Mathematics (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 5012015: | Foundational Skills in Mathematics 3-5 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current)) |
Related Resources
Formative Assessments
| Name | Description |
| Tenths and Hundredths | Students are asked if an equation involving the sum of two fractions is true or false. Then students are asked to find the sum of two fractions. |
| Adding Five Tenths | Students express a fraction with a denominator of 10 as an equivalent fraction with a denominator of 100 and are then asked to add the fraction to another fraction with a denominator of 100. |
| Hundredths and Tenths | Students are asked if an equation is true or false. Then students are asked to find the sum of two fractions. |
| Seven Tenths | Students express a fraction with a denominator of 10 as an equivalent fraction with a denominator of 100 and are then asked to add the fraction to another fraction with a denominator of 100. |
Lesson Plans
| Name | Description |
| Wondrous Water Parks | This activity requires students to apply their knowledge of unit conversions, speed calculation, and comparing fractions to solve the problem of which water park their class should choose to go on for their 5th grade class trip. |
| Playground Picks | In this Model Eliciting Activity, MEA, students will work in groups to determine a procedure for ranking playground equipment to help a school purchase new equipment for their playground. Students will compare fractions with like and unlike denominators and numerators, make decisions based on information given in a data table, and write a letter to the school providing evidence for their decisions. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx |
Original Student Tutorial
| Name | Description |
| Fractions at the Fair: Equivalent Tenths and Hundredths | Learn about equivalent 10ths and 100ths and how to calculate these equivalent fractions at the fair in this interactive tutorial. |
Problem-Solving Tasks
| Name | Description |
| Adding Tenths and Hundredths | The purpose of this task is adding fractions with a focus on tenths and hundredths. |
| How Many Tenths and Hundredths? | The purpose of this task is for students to finish the equations to make true statements. Parts (a) and (b) have the same solution, which emphasizes that the order in which we add doesn't matter (because addition is commutative), while parts (c) and (d) emphasize that the position of a digit in a decimal number is critical. The student must really think to encode the quantity in positional notation. In parts (e), (f), and (g), the base-ten units in 14 hundredths are bundled in different ways. In part (e), "hundredths" are thought of as units: 14 things = 10 things + 4 things. Part (h) addresses the notion of equivalence between hundredths and tenths. |
| Fraction Equivalence | Students may not articulate every detail, but the basic idea for a case like the one shown here is that when you have equivalent fractions, you have just cut the pieces that represent the fraction into more but smaller pieces. Explaining fraction equivalences at higher grades can be a bit more involved (e.g. 6/8=9/12), but it can always be framed as subdividing the same quantity in different ways. |
| Expanded Fractions and Decimals | The purpose of this task is for students to show they understand the connection between fraction and decimal notation by writing the same numbers both ways. Comparing and contrasting the two solutions shown below shows why decimal notation can be confusing. The first solution shows the briefest way to represent each number, and the second solution makes all the zeros explicit. |
| Dimes and Pennies | The purpose of this task is to help students gain a better understanding of fractions through the use of dimes and pennies. |
Tutorials
| Name | Description |
| Adding Two Fractions with Denominators 10 and 100 | The Khan Academy tutorial video presents a visual fraction model for adding 3/10 + 7/100 . |
| Visually Converting from Tenths to Hundredths | In this Khan Academy video a fraction is converted from tenths to hundredths using grid diagrams. |
Student Resources
Original Student Tutorial
| Name | Description |
| Fractions at the Fair: Equivalent Tenths and Hundredths: | Learn about equivalent 10ths and 100ths and how to calculate these equivalent fractions at the fair in this interactive tutorial. |
Problem-Solving Tasks
| Name | Description |
| Adding Tenths and Hundredths: | The purpose of this task is adding fractions with a focus on tenths and hundredths. |
| How Many Tenths and Hundredths?: | The purpose of this task is for students to finish the equations to make true statements. Parts (a) and (b) have the same solution, which emphasizes that the order in which we add doesn't matter (because addition is commutative), while parts (c) and (d) emphasize that the position of a digit in a decimal number is critical. The student must really think to encode the quantity in positional notation. In parts (e), (f), and (g), the base-ten units in 14 hundredths are bundled in different ways. In part (e), "hundredths" are thought of as units: 14 things = 10 things + 4 things. Part (h) addresses the notion of equivalence between hundredths and tenths. |
| Fraction Equivalence: | Students may not articulate every detail, but the basic idea for a case like the one shown here is that when you have equivalent fractions, you have just cut the pieces that represent the fraction into more but smaller pieces. Explaining fraction equivalences at higher grades can be a bit more involved (e.g. 6/8=9/12), but it can always be framed as subdividing the same quantity in different ways. |
| Expanded Fractions and Decimals: | The purpose of this task is for students to show they understand the connection between fraction and decimal notation by writing the same numbers both ways. Comparing and contrasting the two solutions shown below shows why decimal notation can be confusing. The first solution shows the briefest way to represent each number, and the second solution makes all the zeros explicit. |
| Dimes and Pennies: | The purpose of this task is to help students gain a better understanding of fractions through the use of dimes and pennies. |
Tutorials
| Name | Description |
| Adding Two Fractions with Denominators 10 and 100: | The Khan Academy tutorial video presents a visual fraction model for adding 3/10 + 7/100 . |
| Visually Converting from Tenths to Hundredths: | In this Khan Academy video a fraction is converted from tenths to hundredths using grid diagrams. |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Adding Tenths and Hundredths: | The purpose of this task is adding fractions with a focus on tenths and hundredths. |
| How Many Tenths and Hundredths?: | The purpose of this task is for students to finish the equations to make true statements. Parts (a) and (b) have the same solution, which emphasizes that the order in which we add doesn't matter (because addition is commutative), while parts (c) and (d) emphasize that the position of a digit in a decimal number is critical. The student must really think to encode the quantity in positional notation. In parts (e), (f), and (g), the base-ten units in 14 hundredths are bundled in different ways. In part (e), "hundredths" are thought of as units: 14 things = 10 things + 4 things. Part (h) addresses the notion of equivalence between hundredths and tenths. |
| Fraction Equivalence: | Students may not articulate every detail, but the basic idea for a case like the one shown here is that when you have equivalent fractions, you have just cut the pieces that represent the fraction into more but smaller pieces. Explaining fraction equivalences at higher grades can be a bit more involved (e.g. 6/8=9/12), but it can always be framed as subdividing the same quantity in different ways. |
| Expanded Fractions and Decimals: | The purpose of this task is for students to show they understand the connection between fraction and decimal notation by writing the same numbers both ways. Comparing and contrasting the two solutions shown below shows why decimal notation can be confusing. The first solution shows the briefest way to represent each number, and the second solution makes all the zeros explicit. |
| Dimes and Pennies: | The purpose of this task is to help students gain a better understanding of fractions through the use of dimes and pennies. |

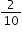 .
.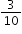 ?
?