General Information
Subject Area: X-Mathematics (former standards - 2008)
Grade: 912
Body of Knowledge: Discrete Mathematics
Idea: Level 1: Recall
Standard: Set Theory - Operate with sets, and use set theory to solve problems.
Date Adopted or Revised: 09/07
Content Complexity Rating:
Level 1: Recall
-
More Information
Date of Last Rating: 06/07
Status: State Board Approved - Archived
Assessed: Yes
Test Item Specifications
N/A
Clarification :
Students will perform set operations such as union and intersection, complement, and cross product.
Students will perform set operations such as union and intersection, complement, and cross product.
Content Limits :
Items may include set notation and symbols from set theory.
Finite sets should contain no more than a total of 15 unordered elements and no more than 30 ordered elements.
If an item follows a numerical pattern, data may be represented by infinite sets. Example: Natural numbers {1, 2, 3, 4 . . .}
Notation for the complement of set A will be limited to A' and ~A.
Stimulus Attributes :
Items may be set in either real-world or mathematical contexts.
Graphics should be used for most of these items, as appropriate.
Sets should list all elements in the stem (e.g., do not use natural numbers between 2 and 5.).
Sample Test Items (2)
| Test Item # | Question | Difficulty | Type |
| Sample Item 1 | The set T represents several Taurine breeds of cattle.
T = {Angus, Devon, Shorthorn, Texas Longhorn} The set Z represents several Zebu breeds of cattle. Z = {Boran, Nelore, Ponwar} What is the total number of elements in the set T × Z ? |
N/A | MC: Multiple Choice |
| Sample Item 2 | Set D lists the ages of Dianna’s grandchildren.
D = {2, 5, 6, 8, 10, 11} Set K lists the ages of Karen’s grandchildren. K = {2, 10, 18} Set P lists the ages of Patrick’s grandchildren. P = {10, 11, 14} 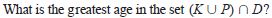 |
N/A | FR: Fill-in Response |
Related Resources
Video/Audio/Animation
| Name | Description |
| MIT BLOSSOMS - Taking Walks, Delivering Mail: An Introduction to Graph Theory | This learning video presents an introduction to graph theory through two fun, puzzle-like problems:"The Seven Bridges of Königsberg" and "The Chinese Postman Problem". Any high school student in a college-preparatory math class should be able to participate in this lesson. Materials needed include: pen and paper for the students; if possible, printed-out copies of the graphs and image that are used in the module; and a blackboard or equivalent. During this video lesson, students will learn graph theory by finding a route through a city/town/village without crossing the same path twice. They will also learn to determine the length of the shortest route that covers all the roads in a city/town/village. To achieve these two learning objectives, they will use nodes and arcs to create a graph and represent a real problem. This video lesson cannot be completed in one usual class period of approximately 55 minutes. It is suggested that the lesson be presented over two class sessions. |
