General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Data Analysis and Probability
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In Algebra I, students studied associations in bivariate categorical data using conditional relative frequencies. In Math for College Liberal Arts, students work in more depth with conditional probabilities and independence in real-world contexts.- Instruction includes tasks asking students to explain the meaning of independence in a simple context, as well as what it would mean for two events to not be independent. Students should analyze and think critically about relationships between two events that may or may not appear to be related.
- Provide common examples of independent and dependent events and ask students to
provide examples of their own for both cases.
- Independent: Lisa ate breakfast, and she went to school.
- Dependent: Jim loaded his videogame disk, and started playing his videogame.
- Remind students that given data, independence can be calculated, or verified. In some
cases, situations that intuitively seem independent, may be correlated. Emphasize that this
correlation does not imply cause or dependence, but rather only shows that the two events
are not independent. (Refer to MA.912.DP.1.3 from Algebra I.) Two-way tables can be
used to assist with this discussion.
- For example, ask students to answer a series of questions based on given data.
The table below shows caffeine preference for mathematics and engineering
students based on a survey of 200 college students.Students can describe two conditional probabilities in everyday language that can be determined from the “Mathematics” row in the table. Everyday language could include the probability of choosing a student who prefers coffee given they are math major; or of those who are math majors choosing an energy drinker. Students can describe two conditional probabilities in everyday language that can be determined from the “Coffee” column in the table. Everyday language could include the probability of choosing a student who is a math major given they drink coffee; or the probability of choosing an engineering student from the coffee drinkers.
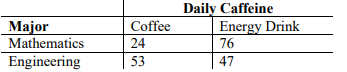
Students can determine whether students with a mathematics major more likely to drink coffee or if students with an engineering major are. To do so, students would need to determine if the events are independent (MA.912.DP.4.4).
- For example, ask students to answer a series of questions based on given data.
The table below shows caffeine preference for mathematics and engineering
students based on a survey of 200 college students.
- Students use their prior knowledge of the word independent to mean not relying on another, and believe that conditional probabilities should be different when events are independent. Emphasize that having equivalent conditional probabilities means the probability of an event is the same no matter whether the other event occurs.
Common Misconceptions or Errors
- Students misinterpret the word independence in relation to probability.
- Students may believe equal conditional probabilities means two events depend on each other in order to be the same. To address this misconception, discuss the meaning in context to emphasize the probability of one event is just as likely whether the other event occurs or not.
- Students may assume independence based on the description of the events alone.
Instructional Tasks
Instructional Task 1 (MTR.7.1)- One hundred people were surveyed and asked their preference for watching movies via streaming services or a movie theater. The results are shown in the table below.
- Part A. Describe three possible conditional probabilities using everyday language given this table.
- Part B. Find the probability that a person surveyed prefers streaming.
- Part C. Find the probability that a person surveyed prefers streaming given they are a child.
- Part D. Are the events of prefers streaming and being a child independent? Explain.
Instructional Items
Instructional Item 1- Part A. Today there is a 55% chance of rain, a 20% chance of lightning, and a 15% chance of lightning and rain together. Are the two events “rain today” and “lightning today” independent events? Justify your answer.
- Part B. Now suppose that today there is a 60% chance of rain, a 15% chance of lightning, and a 20% chance of lightning if it’s raining. What is the chance of both rain and lightning today?