Standard #: MA.912.GR.5.2


This document was generated on CPALMS - www.cpalms.org



Construct the bisector of a segment or an angle, including the perpendicular bisector of a line segment.


Clarifications


Clarification 1: Instruction includes using compass and straightedge, string, reflective devices, paper folding or dynamic geometric software.

General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Geometric Reasoning
Standard: Make formal geometric constructions with a variety of tools and methods.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Angle

 

Vertical Alignment

Previous Benchmarks

Next Benchmarks

 

Purpose and Instructional Strategies

In elementary grades, students drew lines and angles using a variety of tools, including rulers and protractors, and by making measurements with those tools, they could bisect lines and angles. In Geometry, students are introduced to constructions that do not rely on making measurements, specifically bisecting an angle and bisecting a segment, including perpendicular bisectors, using a compass and straightedge. These two procedures are embedded within constructing an inscribed circle and a circumscribed circle of a triangle as well as in the construction of a square inscribed in a circle.  
  • Instruction includes the use of manipulatives, tools and geometric software. Allowing students to explore constructions with dynamic software reinforces why the constructions work. 
    • For example, the use of paper folding (e.g., patty paper) can be used to determine the angle bisector of a given angle and the midpoint or perpendicular bisector of a given segment. 
  • Instruction includes the connection to triangle congruence when constructing an angle bisector. 
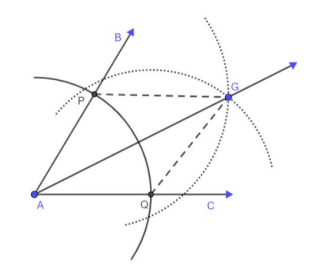
    • For example, have students place the compass at point A and draw an arc intersecting the sides of the angle resulting in the points of intersection P and Q. Students should realize that AP ≅ AQ. Without changing the compass setting, add two arcs intersecting in the interior of the angle at the point G. Students should realize that PG ≅ QG By the Reflexive property of congruence,  AG ≅ AG Therefore, ΔAPG ≅ ΔAQG by SSS and since corresponding parts of congruent triangles are congruent (CPCTC), ∠PAG ≅ ∠QAG and AG is the angle bisector of ∠BAC. 
  • Instruction includes the connection to the converse of the Perpendicular Bisector Theorem when constructing a perpendicular bisector. 
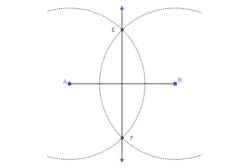
    • For example, students can set the compass width more than half the length of AB. Students can draw arcs intersecting above and below the segment at points E and F. Therefore, AE ≅ BE and  AF ≅  BF. That is, points E and F are each the same distance to the endpoints of AB and that means they lie on the Perpendicular Bisector. 
  • Instruction includes the student understanding that when one has constructed the perpendicular bisector, they have also constructed the midpoint of a segment. (MTR.2.1) 
    • For example, using the same steps as in the last construction, the midpoint of the segment can be identified as the point where the perpendicular bisector meets the segment. 
  • Instruction includes the connection to logical reasoning and visual proofs when verifying that a construction works. 
    • For example, once the construction of the perpendicular bisector is completed, discuss with students how this construction and a compass can be used to experimentally check the Perpendicular Bisector Theorem. (MA.912.GR.1.1) 
  • For expectations of this benchmark, constructions should be reasonably accurate and the emphasis is to make connections between the construction steps and the definitions, properties and theorems supporting them. 
  • While going over the steps of geometric constructions, ensure that students develop vocabulary to describe the steps precisely. (MTR.4.1) 
  • Instruction includes the connection between constructions and properties of quadrilaterals, including rhombi. 
    • For example, when constructing the angle bisector, if the compass width is not changed throughout the process, then quadrilateral AHGF is a rhombus since it has 4 equal sides ( AH HG, GF FA). The diagonals of a rhombus bisect opposite angles. Therefore, ∠HAF is bisected by the diagonal of the rhombus AG and AG is the angle bisector of ∠BAC. Similarly, when constructing the perpendicular bisector, it can be seen that the diagonals of a rhombus are perpendicular. 
  • Instruction includes the student understanding that in a geometric construction, one does not use the markings on a ruler or on a protractor to bisect a segment or angle. Students should realize that there are limitations on precision that are inherent in the markings on rulers or protractors. 
  • It is important to build the understanding that formal constructions are valid when the lengths of segments or measures of angles are not known, or have values that do not appear on a ruler or protractor, including irrational values. 
  • Problem types include identifying the next step of a construction, a missing step in a construction or the order of the steps in a construction.

 

Common Misconceptions or Errors

  • Students may not make the connection that any point on the perpendicular bisector is equidistant from the endpoints of the segment, not just the midpoint of the segment. 
  • Students may not understand why they are not using rulers and protractors to bisect segments and angles.

 

Instructional Tasks

Instructional Task 1 (MTR.7.1) 
  • A map of some popular universities is shown below. 
  
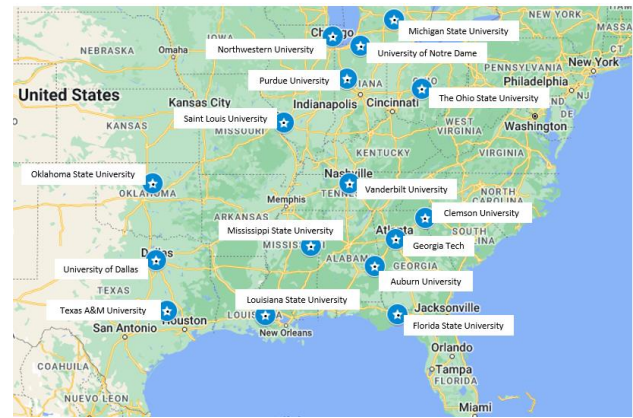
    • Part A. Prove that Georgia Tech is approximately equidistant from Clemson University and Auburn University. 
    • Part B. Find one or more universities that are approximately equidistant from Florida State University and Oklahoma State University?

 

Instructional Items

Instructional Item 1 
  • An image is provided below. 
    • Part A. Construct the bisector of angle D. 
    • Part B. Construct the midpoint of segment DB.

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.


Related Courses

Course Number1111 Course Title222
1200400: Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206310: Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206320: Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206315: Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7912065: Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.912.GR.5.AP.2 Construct the bisector of a segment, including the perpendicular bisector of a line segment.


Related Resources

Formative Assessments

Name Description
Bisecting a Segment and an Angle

Students are asked to construct the bisectors of a given segment and a given angle and to justify one of the steps in each construction.

Constructions for Perpendicular Lines

Students are asked to construct a line perpendicular to given line (1) through a point not on the line and (2) through a point on the line.

Lesson Plans

Name Description
Geometric Construction Site

This lesson takes students from simple construction of line segments and angles to an optional extension worksheet for creating triangles.

Keeping Triangles in Balance: Discovering Triangle Centroid is Concurrent Medians

In this lesson, students identify, analyze, and understand the Triangle Centroid Theorem. Students discover that the centroid is a point of concurrency for the medians of a triangle and recognize its associated usage with the center of gravity or barycenter. This set of instructional materials provides the teacher with hands-on activities using technology as well as paper-and-pencil methods.

Construction of Inscribed Regular Hexagon

A GeoGebra lesson for students to become familiar with computer based construction tools. Students work together to construct a regular hexagon inscribed in a circle using rotations. Directions for both a beginner and advanced approach are provided.

Copying and Bisecting an Angle

This lesson is a gradual release model for constructing congruent angles and bisecting angles.

Inscribe Those Rims

This lesson will engage students with an interactive and interesting way to learn how to inscribe polygons in circles.

Bisecting Angles And Line Segments

This construction lesson will teach students how to bisect an angle and how to find the perpendicular bisector of a segment using a compass and straightedge.

Construction Junction

Students will learn how to construct an equilateral triangle and a regular hexagon inscribed in a circle using a compass and a straightedge.

Triangle Medians

This lesson will have students exploring different types of triangles and their medians. Students will construct mid-points and medians to determine that the medians meet at a point.

Inscribe it

This activity allows students to practice the construction process inscribing a regular hexagon and an equilateral triangle in a circle using GeoGebra software.

Construct Regular Polygons Inside Circles

Students will be able to demonstrate that they can construct, using the central angle method, an equilateral triangle, a square, and a regular hexagon, inscribed inside a circle, using a compass, straightedge, and protractor. They will use worksheets to master the construction of each polygon, one inside each of three different circles. As an extension to this lesson, if computers with GeoGebra are available, the students should be able to perform these constructions on computers as well.

Construct This

In this lesson, students will construct a square inscribed in a circle using the properties of a square and determine if there is more than one way to complete the construction.

I Am Still Me Transformed.

Students explore ways of applying, identifying, and describing reflection and rotation symmetry for both geometric and real-world objects, for them to develop a better understanding of symmetries in transformational geometry.

Constructing an Angle Bisector

Students construct an angle bisector given a straightedge and compass then verify their process. The Guided Practice is done in stations. One that is teacher-led and one that is student-led. In order to complete the student-led Guided Practice, access to a teacher computer and projector is needed. Then the students independently create their own angle and its bisector and verify their work for a grade. Students use patty paper and protractors to confirm the accuracy of the construction.

Determination of the Optimal Point

Students will use dynamic geometry software to determine the optimal location for a facility under a variety of scenarios. The experiments will suggest a relation between the optimal point and a common concept in geometry; in some cases, there will be a connection to a statistical concept. Algebra can be used to verify some of the conjectures.

Back to the Basics: Constructions

Students will use a compass and straightedge to develop methods for constructions. GeoGebra directions are also provided.

Sage and Scribe - Points, Lines, and Planes

Students will practice using precise definitions while they draw images of Points, Lines, and Planes. Students will work in pairs taking turns describing an image while their partner attempts to accurately draw the image.

Fundamental Property of Reflections

This lesson helps students discover that in a reflection, the line of reflection is the perpendicular bisector of any segment connecting any pre-image point with its reflected image.

What's the Point? Part 2

In this lesson, students use a paper-folding technique to discover the properties of angle bisectors. At the conclusion of the activity, students will be able to compare/contrast the points of concurrency of perpendicular and angle bisectors.

Off on a Tangent

Students learn and apply vocabulary, notation, concepts, and geometric construction techniques associated with circles and their tangents to a historical real-world scenario, the Mason-Dixon Line, and a hypothetical real-world scenario, the North-South Florida Line.

Circumnavigating the Circumcenter

Students use the concurrent point of perpendicular bisectors of triangle sides to determine the circumcenter of three points. Students will reason that the circumcenter of the vertices of a polygon is the optimal location for placement of a facility to service all of the needs of sites at the vertices forming the polygon.

Crafty Circumference Challenge

Students learn about geometric construction tools and how to use them. Students will partition the circumference of a circle into three, four, and six congruent arcs which determine the vertices of regular polygons inscribed in the circle. An optional project is included where students identify, find, and use recycled, repurposed, or reclaimed objects to create "crafty" construction tools.

Right turn, Clyde!

Students will develop their knowledge of perpendicular bisectors & point of concurrency of a triangle, as well as construct perpendicular bisectors through real world problem solving with a map.

Halfway to the Middle!

Students will develop their knowledge of mid-segments of a triangle, construct and provide lengths of mid-segments.

Location, Location, Location, Location?

Students will use their knowledge of graphing concurrent segments in triangles to locate and identify which points of concurrency are associated by location with cities and counties within the Texas Triangle Mega-region.

St. Pi Day construction with a compass & ruler

St. Pi Day construction with compass

This activity uses a compass and straight-edge(ruler) to construct a design. The design is then used to complete a worksheet involving perimeter, circumference, area and dimensional changes which affect the scale factor ratio.

Concurrent Points Are Optimal

Students will begin with a review of methods of construction of perpendicular bisectors and angle bisectors for the sides of triangles. Included in the review will be a careful discussion of the proofs that the constructions actually produce the lines that were intended.

Next, students will investigate why the perpendicular bisectors and angle bisector are concurrent, that is, all three meet at a single meet.

A more modern point of currency is the Fermat-Torricelli point (F-T). The students will construct (F-T) in GeoGebra and investigate limitations of its existence for various types of triangles.

Then a set of scenarios will be provided, including some one-dimensional and two-dimensional situations. Students will use GeoGebra to develop conjectures regarding whether a point of concurrency provides the solution for the indicated situation, and which one.

A physical model for the F-T will be indicated. The teacher may demonstrate this model but that requires three strings, three weights, and a base that has holes. A recommended base is a piece of pegboard (perhaps 2 feet by 3 feet), the weights could be fishing weights of about 3 oz., the string could be fishing line; placing flexible pieces of drinking straws in the holes will improve the performance.

The combination of geometry theorems, dynamic geometry software, a variety of contexts, and a physical analog can provide a rich experience for students.

What's the Point? Part 1

This is a patty paper-folding activity where students measure and discover the properties of the point of concurrency of the perpendicular bisectors of the sides of a triangle.

Original Student Tutorials

Name Description
Angle UP: Player 1

Explore the construction processes for constructing an angle bisector, copying an angle and constructing a line parallel to a given line through a point not on the line using a variety of tools in this interactive, retro video game-themed tutorial.

NOTE: This tutorial uses both the angle bisector construction and the construction to copy an angle as an extension opportunity to also construct a line parallel to a given line through a point not on the line. Students also learn to identify corresponding angles created when a transversal crosses parallel lines, and discover using Geogebra that these angles are congruent.

Meet Me Half Way

Plan a paddle board expedition by learning how to do basic geometric constructions including copying a segment, constructing a segment bisector, constructing a segment's perpendicular bisector and constructing perpendicular segments using a variety of tools in this interactive tutorial.

The Blueprints of Construction

Learn to construct the perpendicular bisector of a line segment using a straightedge and compass with this interactive tutorial.

Perspectives Video: Teaching Ideas

Name Description
Geometric Constructions- Angle Bisector

Unlock an effective teaching strategy for making connections in geometric constructions in this Teacher Perspectives video for educators.

Perpendicular Bisectors & Constructions

Unlock an effective teaching strategy for teaching geometric constructions, specifically perpendicular bisectors, in this Teacher Perspectives video for educators.

Problem-Solving Tasks

Name Description
Construction of perpendicular bisector

This problem solving task challenges students to construct a perpendicular bisector of a given segment.

Bisecting an angle

This problem solving task challenges students to bisect a given angle.

Locating Warehouse

This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines).

Angle bisection and midpoints of line segments

This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts.

Student Resources

Original Student Tutorials

Name Description
Angle UP: Player 1:

Explore the construction processes for constructing an angle bisector, copying an angle and constructing a line parallel to a given line through a point not on the line using a variety of tools in this interactive, retro video game-themed tutorial.

NOTE: This tutorial uses both the angle bisector construction and the construction to copy an angle as an extension opportunity to also construct a line parallel to a given line through a point not on the line. Students also learn to identify corresponding angles created when a transversal crosses parallel lines, and discover using Geogebra that these angles are congruent.

Meet Me Half Way:

Plan a paddle board expedition by learning how to do basic geometric constructions including copying a segment, constructing a segment bisector, constructing a segment's perpendicular bisector and constructing perpendicular segments using a variety of tools in this interactive tutorial.

The Blueprints of Construction:

Learn to construct the perpendicular bisector of a line segment using a straightedge and compass with this interactive tutorial.

Problem-Solving Tasks

Name Description
Construction of perpendicular bisector:

This problem solving task challenges students to construct a perpendicular bisector of a given segment.

Bisecting an angle:

This problem solving task challenges students to bisect a given angle.

Locating Warehouse:

This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines).

Angle bisection and midpoints of line segments:

This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts.



Parent Resources

Problem-Solving Tasks

Name Description
Construction of perpendicular bisector:

This problem solving task challenges students to construct a perpendicular bisector of a given segment.

Bisecting an angle:

This problem solving task challenges students to bisect a given angle.

Locating Warehouse:

This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines).

Angle bisection and midpoints of line segments:

This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts.



Printed On:4/23/2024 11:49:36 AM
Print Page | Close this window