General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Geometric Reasoning
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Angle
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In elementary grades, students drew lines and angles using a variety of tools, including rulers and protractors. In Geometry, students are introduced to constructions for the first time, specifically copying a segment or an angle. These two procedures are embedded in other basic constructions, and the concept of constructing and identifying copies of segments and angles is closely connected to visualizing and understanding congruence.- Instruction includes the use of manipulatives, tools and geometric software. Allowing
students to explore constructions with dynamic software reinforces why the constructions
work.
- For example, students can use tracing/folding paper (e.g., patty paper) to trace the copy of an angle, or the copy of a segment, and verify that the angle and its copy are congruent, or that the segment and its copy are congruent. Additionally, using several folds, it is possible to verify the congruency of two angles or two segments drawn on the same piece of paper.
- Instruction includes the connection to logical reasoning and visual proofs when verifying that a construction works.
- Instruction includes discussing the role of the compass in a geometric construction,
beyond drawing circles, and how a string can replace a compass. Most of the time in this
course, compasses will be used to draw arcs. Discuss how no matter the point chosen on
the arc, the distance to the given point is the same.
- For example, students can place the compass at P and draw an arc. Choosing two points on the arc, A and B, the distance to P is the same, AP = BP and AP ≅ BP are radii of the circle containing the drawn arc centered at P.
- Instruction includes the student understanding that in a geometric construction, one does not use the markings on a ruler or on a protractor to copy a segment or angle. Students should realize that there are limitations on precision that are inherent in the markings on rulers or protractors.
- It is important to build the understanding that formal constructions are valid when the lengths of segments or measures of angles are not known, or have values that do not appear on a ruler or protractor, including irrational values.
- For expectations of this benchmark, constructions should be reasonably accurate and the emphasis is to make connections between the construction steps and the definitions, properties and theorems supporting them.
- While going over the steps of geometric constructions, ensure that students develop vocabulary to describe the steps precisely. (MTR.4.1)
- Problem types include identifying the next step of a construction, a missing step in a construction or the order of the steps in a construction.
Common Misconceptions or Errors
- Students may not understand that the size of the angle, “the opening,” is what is being measured when copying an angle.
- Students may not understand why they are not using the marking on rulers and protractors to copy segments and angles.
Instructional Tasks
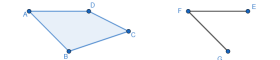
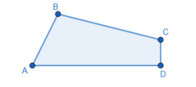
Instructional Task 1 (MTR.2.1, MTR.3.1)- Create a construction of quadrilateral JKLM so that it is congruent to quadrilateral ABCD.
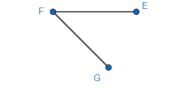
Instructional Task 2 (MTR.2.1, MTR.5.1)
- Given angle EFG below, create a copy so that it creates parallelogram EFGH.
Instructional Items
Instructional Item 1- Construct the necessary segments and angles to construct quadrilateral EFGH so that it is congruent to quadrilateral EFGH. Assume ∠DAB ≅ ∠EFG, DA ≅ EF and AB ≅ FG.
