General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Circle
- Diameter
- Quadrilateral
- Radius
- Slope
- Triangle
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8 and Algebra 1, students used coordinate systems to study lines and the find distances between points. In Geometry, students expand on their knowledge of coordinate geometry to solve problems geometric problems in real-world and mathematical contexts. In later courses, coordinates will be used to solve a variety of problems involving many shapes, including conic sections and shapes that can be studied using polar coordinates.- Problem types include finding the midpoint of a segment (midpoint formula); partitioning a segment given endpoints and a ratio; writing the equation of a line, including lines that are parallel or perpendicular; finding the coordinates of the centroid of a triangle; and finding the distance between two points. In some cases, students may need to utilize systems of equations in order to determine solutions.
- Instruction includes the definition of a tangent to a circle and its properties, and the definition of the medians of a triangle and their point of concurrency (centroid).
- Instruction includes various approaches when finding the coordinates of a point
partitioning a directed line segment (given the endpoints). (MTR.2.1, MTR.3.1) Different methods are described below.
- The first concept that can be discussed is the connection to weighted average of
two points. If the given ratio is a: b, that means the weights of the endpoints (1 + 1) and (2 + 2) are and , respectively.
- For example, if the given ratio is 2: 3 and the points are at A(−3, 6) and B(4,−8) discuss with students where P is on its way from A to B. Students should be able to come with . That means the weight of A is and the weight of B is . The next step is to calculate the -coordinate of P using the weighted averages: p = x1 + 2 which is equivalent to p = (−3) + (4) which is equivalent to p = −. Then calculate the -coordinate of P using the weighted averages: p = 1 + 2 which is equivalent to p = (6) + (−8). Therefore, P is at (− , ).
- The second method uses the computations of a fraction of the horizontal and the
vertical distance between the endpoints (partial distances). That is, if P is partitioning the segment in the ratio a : b or of the way from ( 1 , 1) to (2 , 2) then its location is of the horizontal distance and of the vertical distance from (1 , 1) to (2 , 2).
- For example, if the given ratio is 2: 3 and the points are at A(−3, 6) and B(4,−8) discuss with students where P is on its way from A to B. Students should be able to determine the horizontal distance from A to B as 2 - 1 = 4 − (−3), which is 7. Then, determine the vertical distance 2 as 2 – 1 = −8 − 6, which is −14. Since the ratio is 2: 3, P is of the way from A to B. Students can calculate of the horizontal and the vertical distance, (7) = and −14) = −, respectively. Students should realize that they will need to add the partial distances to A. Therefore, the coordinates of P are (−3 + , 6 − ) = (− , ).
- Other methods include the use of formulas. It is important to note that this would require students to memorize formulas and not encourage students to explore all of the concepts.
- The first concept that can be discussed is the connection to weighted average of
two points. If the given ratio is a: b, that means the weights of the endpoints (1 + 1) and (2 + 2) are and , respectively.
- Instruction include that understanding that the midpoint of a segment partitions that segment in the ratio 1:1.
- Instruction includes various approaches when finding medians or centroids of triangles.
(MTR.2.1, MTR.3.1) Different methods are described below.
- The equation of the line containing a median can be written from the coordinates of the vertex and the coordinates of the midpoint of the opposite side. Solving a system of equations formed by the equations of the two lines containing two medians of a triangle will result in the coordinates of the centroid.
- The centroid formula can be given as Centroid =
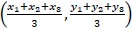 , where (1 , 1),(2 , 2) and (3 + y3) are the coordinates of the vertices of the triangle.
Connections should be made to the fact that the coordinates of the centroid are the
means of the coordinates of the vertices.
, where (1 , 1),(2 , 2) and (3 + y3) are the coordinates of the vertices of the triangle.
Connections should be made to the fact that the coordinates of the centroid are the
means of the coordinates of the vertices. - The centroid is also the center of gravity of the triangle. Show them with a cardboard triangle that the triangle balances perfectly on its centroid (use a pencil or the tip of your finger).
- A method that makes connections to partitions can be found in the Centroid
2 Theorem. This theorem states that the centroid is of the distance from each
3
vertex to the midpoint of the opposite side, that is, the centroid partitions the
2 median of the way from the vertex to the midpoint of the opposite side. This 3
theorem can also be used to find the coordinates of centroid.
- For example, given a triangle with vertices A(1 + 1), B(2 + 2) and C(3 + 3), the midpoints of the sides will be A (a1 + b1) , N (a2 + b2) and L (a3 + b3) for BC, AC and AB, respectively. Applying the Centroid Theorem to the median LC, the centroid is at ( 3 + a3, 3 + b3). Using Substitution property of equality,
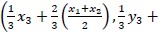
 =
= 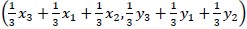 . This results in Centroid =
. This results in Centroid = 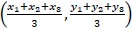 .
.
- For example, given a triangle with vertices A(1 + 1), B(2 + 2) and C(3 + 3), the midpoints of the sides will be A (a1 + b1) , N (a2 + b2) and L (a3 + b3) for BC, AC and AB, respectively. Applying the Centroid Theorem to the median LC, the centroid is at ( 3 + a3, 3 + b3). Using Substitution property of equality,
- The centroid formula can be given as Centroid =
Common Misconceptions or Errors
- Students may confuse using vertical and horizontal distances when partitioning segments.
- Students may need to be reminded that the segment partition refers to the parts, whose
sum is the whole, not a part of a whole.
- For example, a segment partitioned in a 1:4 ratio is actually 5 parts separated into 1 part and 4 parts, not 1 out of 4 parts.
Instructional Tasks
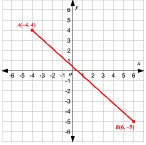
Instructional Task 1 (MTR.3.1)- What are the coordinates of the point that partitions segment AB in the ratio 2: 3?
- Circle A has center located at (2, 2) and contains the point (4,4).
- Part A. Write the equation that describes circle A.
- Part B. Write the equation of a line tangent to Circle A at (4,4).
- Part C. Find the equation of a vertical tangent line and of a horizontal tangent line.
- Triangle ABC has two of its the vertices located at (−4,−1) and (3,−3).
- Part A. Triangle ABC has a centroid located at (−1, ). What is the third vertex of the triangle?
- Part B. Determine whether triangle ABC is a right triangle based on its angle measures and side lengths.
- Part C. If triangle ABC is not a right triangle, can you classify what type of triangle ABC is?
Instructional Items
Instructional Item 1- Given J(−4,2) and K(2,1), find the coordinates of point M on JK that partitions the segment into the ratio 1: 2.

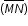 so that P partitions
so that P partitions