General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Geometric Reasoning
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Coordinate Plane
- Origin
- Reflection
- Rigid Transformation
- Rotation
- Translation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students first learned to associate congruence and similarity with reflections, rotations, translations and dilations. In Geometry, students learn that these transformations provide an equivalent alternative to using congruence and similarity criteria for triangles.- Instruction includes the connection to the Side-Angle-Side, Angle-Side-Angle (and Angle-Angle-Side), Hypotenuse-Leg and Side-Side-Side congruence criteria. It may be helpful for students to work through one transformation at a time to determine congruence. One approach would be to begin with a translation to map one of the vertices of one triangle to the corresponding vertex of the other. Then, if necessary, a rotation about the first vertex can be used to map a second vertex of one triangle to the corresponding vertex of the other. Finally, it may be necessary to use a reflection to match the corresponding third vertices.
- For example, triangles ABC and PQR are given below, with AB ≅ PQ, BC ≅ QR and AC ≅ PR.One method to prove the triangles are congruent is as follows: The first step is to discuss the transformations that would map AB onto PQ. Students should be able to identify a convenient sequence of a translation and a rotation, both rigid motions, that will accomplish it. Therefore PQ ≅ A′B′ since rigid motions preserve distances.
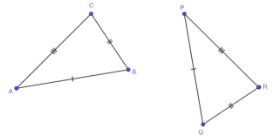Applying the same sequence of transformations to point C only, results in AB ≅ A′B′, BC ≅ B′C′ and AC ≅ A′C′.
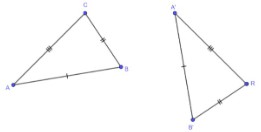In order to prove that the triangles are congruent, there may be two situations.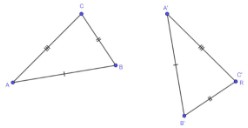
Situation A: Point C has already been mapped to point R from the previous sequence. In this case, use the transitive property of congruence, if BC ≅ QR and BC ≅ B′C′, then QR ≅ B′C′, and if AC ≅ PR and AC ≅ A′C′, then PR ≅ A′C′ proving triangles ABC and PQR are congruent using transformations.
Situation B: If Point C has not already been mapped to point R from the previous sequence, like shown below, one must use a reflection.To prove that C′ can be mapped onto R using a reflection, use the converse of the Perpendicular Bisector Theorem. A′B′ is the perpendicular bisector of C′R′ since PR ≅ A′C′ (and QR ≅ B′C′). Therefore, C′D′ ≅ DR and C′ can be mapped onto R using a reflection over A′B′ proving triangles ABC and PQR are congruent using transformations.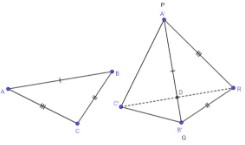
- For example, triangles ABC and PQR are given below, with AB ≅ PQ, BC ≅ QR and AC ≅ PR.
Common Misconceptions or Errors
- Students may have difficulty understanding the value of having two different, equivalent approaches to proving congruence and similarity. Discuss how approaching a situation in different ways deepens understanding. (MTR.2.1)
Instructional Tasks
Instructional Task 1 (MTR.2.1, MTR.4.1)- Triangles ABC and DEF are shown below and AB ≅ EF, ∠B ≅ ∠E and ∠A ≅ ∠F.
- Part A. Describe a sequence of rigid transformations that maps triangle ABC onto triangle DEF.
- Part B. Compare your sequence with a partner. What do you notice? What information about these triangles makes it possible to determine the rigid transformations in Part A?
Instructional Task 2 (MTR.4.1)
- When applying the transformation (, ) → ( + 4, − 6), segment AB maps onto segment LN and segment AC maps onto segment LM.
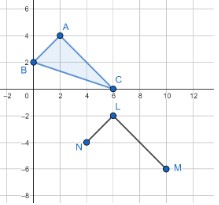
- Part A. How can ΔACB ≅ ΔLMN be proved using one of the congruence criteria?
- Part B. How can ΔACB ≅ ΔLMN be proved using rigid transformations?
Instructional Items
Instructional Item 1- Use the image below to complete the sentence.If NP ≅
, ∠P ≅ and MP ≅ , then there is a sequence of rigid transformations that maps ΔKJL onto .
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.