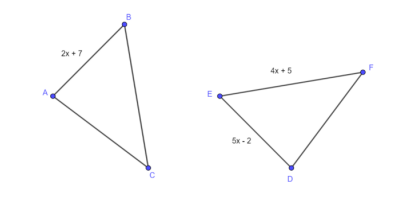
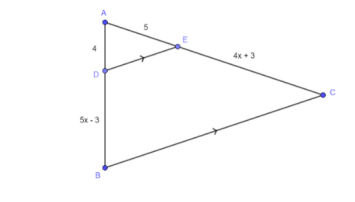
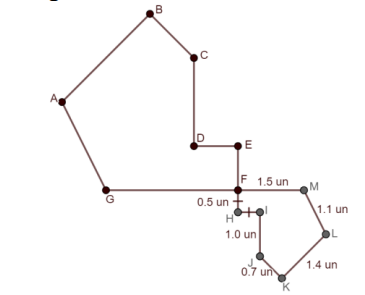
Solve mathematical and real-world problems involving congruence or similarity in two-dimensional figures.
Instruction includes demonstrating that two-dimensional figures are congruent or similar based on given information.
| Name |
Description |
| Transformation and Similarity | Using non-rigid motions (dilations), students learn how to show that two polygons are similar. Students will write coordinate proofs confirming that two figures are similar. |
| Proof of Quadrilaterals in Coordinate Plane | This lesson is designed to instruct students on how to identify special quadrilaterals in the coordinate plane using their knowledge of distance formula and the definitions and properties of parallelograms, rectangles, rhombuses, and squares. Task cards, with and without solution-encoded QR codes, are provided for cooperative group practice. The students will need to download a free "QR Code Reader" app onto their SmartPhones if you choose to use the cards with QR codes. |
| To Be or Not to Be a Parallelogram | Students apply parallelogram properties and theorems to solve real world problems. The acronym, P.I.E.S. is introduced to support a problem solving strategy, which involves drawing a Picture, highlighting important Information, Estimating and/or writing equation, and Solving problem. |
| What's the Problem | Students solve problems using triangle congruence postulates and theorems. |
| Diagonally Half of Me! | This lesson is an exploration activity assisting students prove that diagonals of parallelograms bisect each other. It allows them to compare other quadrilaterals with parallelograms in order to make conjectures about the diagonals of parallelograms. |
| Proving Parallelograms Algebraically | This lesson reviews the definition of a parallelogram and related theorems. Students use these conditions to algebraically prove or disprove a given quadrilateral is a parallelogram. |
| How Do You Measure the Immeasurable? | Students will use similar triangles to determine inaccessible measurements. Examples include exploring dangerous caves and discovering craters on Mars. |
| Proving quadrilaterals algebrically using slope and distance formula | Working in groups, students will prove the shape of various quadrilaterals using slope, distance formula, and polygon properties. They will then justify their proofs to their classmates. |
| Quadrilaterals and Coordinates | In this lesson, students will use coordinates to algebraically prove that quadrilaterals are rectangles, parallelograms, and trapezoids. A through introduction to writing coordinate proofs is provided as well as plenty of practice. |
| Triangles on a Lattice | In this activity, students will use a 3x3 square lattice to study transformations of triangles whose vertices are part of the lattice. The tasks include determining whether two triangles are congruent, which transformations connect two congruent triangles, and the number of non-congruent triangles (with vertices on the lattice) that are possible. |
| Proving Quadrilaterals | This lesson provides a series of assignments for students at the Getting Started, Moving Forward, and Almost There levels of understanding for the Mathematics Formative Assessment System (MFAS) Task Describe the Quadrilateral (CPALMS Resource ID#59180). The assignments are designed to "move" students from a lower level of understanding toward a complete understanding of writing a coordinate proof involving quadrilaterals. |
| Congruence vs. Similarity | Students will learn the difference between congruence and similarity of classes of figures (such as circles, parallelograms) in terms of the number of variable lengths in the class. A third category will allow not only rigid motions and dilations, but also a single one-dimensional stretch, allowing more classes of figures to share sufficient common features to belong. |
| Polygon...Prove it | While this is an introductory lesson on the standard, students will enjoy it, as they play "Speed Geo-Dating" during the Independent practice portion. Students will use algebra and coordinates to prove rectangles, rhombus, and squares. Properties of diagonals are not used in this lesson. |
| Let's Prove the Pythagorean Theorem | Students will use Triangle Similarity to derive the proof of the Pythagorean Theorem and apply this method to develop the idea of the geometric mean with respect to the relationships in right triangles. |
| Altitude to the Hypotenuse | Students will discover what happens when the altitude to the hypotenuse of a right triangle is drawn. They learn that the two triangles created are similar to each other and to the original triangle. They will learn the definition of geometric mean and write, as well as solve, proportions that contain geometric means. All discovery, guided practice, and independent practice problems are based on the powerful altitude to the hypotenuse of a right triangle. |
| Evaluating Statements About Length and Area | This lesson unit is intended to help you assess how well students can understand the concepts of length and area, use the concept of area in proving why two areas are or are not equal and construct their own examples and counterexamples to help justify or refute conjectures. |
| Mirror, Mirror on the ... Ground? | This activity allows students to go outdoors to measure the height of objects indirectly. Similar right triangles are formed when mirrors are placed on the ground between the object that needs to be measured and the student observing the object in the mirror. Students work in teams to measure distances and solve proportions.
This activity can be used as a review or summative assessment after teaching similar triangles. |
| Name |
Description |
| Bank Shot | This task asks students to use similarity to solve a problem in a context that will be familiar to many, though most students are accustomed to using intuition rather than geometric reasoning to set up the shot. |
| Extensions, Bisections and Dissections in a Rectangle | This task involves a reasonably direct application of similar triangles, coupled with a moderately challenging procedure of constructing a diagram from a verbal description. |
| Solar Eclipse | This problem solving task encourages students to explore why solar eclipses are rare by examining the radius of the sun and the furthest distance between the moon and the earth. |
| Mt. Whitney to Death Valley | This task engages students in an open-ended modeling task that uses similarity of right triangles. |
| Joining two midpoints of sides of a triangle | Using a triangle with line through it, students are tasked to show the congruent angles, and conclude if one triangle is similar to the other. |
| Unit Squares and Triangles | This problem solving task asks students to find the area of a triangle by using unit squares and line segments. |
| When Does SSA Work to Determine Triangle Congruence? | In this problem, we considered SSA. The triangle congruence criteria, SSS, SAS, ASA, all require three pieces of information. It is interesting, however, that not all three pieces of information about sides and angles are sufficient to determine a triangle up to congruence. |
| Inscribing a square in a circle | This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context. |
| Construction of perpendicular bisector | This problem solving task challenges students to construct a perpendicular bisector of a given segment. |
| Reflected Triangles | This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected. |
| Right triangles inscribed in circles II | This problem solving task asks students to explain certain characteristics about a triangle. |
| Locating Warehouse | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Angle bisection and midpoints of line segments | This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts. |
| Is This a Rectangle? | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |
| Name |
Description |
| Bank Shot: | This task asks students to use similarity to solve a problem in a context that will be familiar to many, though most students are accustomed to using intuition rather than geometric reasoning to set up the shot. |
| Extensions, Bisections and Dissections in a Rectangle: | This task involves a reasonably direct application of similar triangles, coupled with a moderately challenging procedure of constructing a diagram from a verbal description. |
| Solar Eclipse: | This problem solving task encourages students to explore why solar eclipses are rare by examining the radius of the sun and the furthest distance between the moon and the earth. |
| Mt. Whitney to Death Valley: | This task engages students in an open-ended modeling task that uses similarity of right triangles. |
| Joining two midpoints of sides of a triangle: | Using a triangle with line through it, students are tasked to show the congruent angles, and conclude if one triangle is similar to the other. |
| Unit Squares and Triangles: | This problem solving task asks students to find the area of a triangle by using unit squares and line segments. |
| When Does SSA Work to Determine Triangle Congruence?: | In this problem, we considered SSA. The triangle congruence criteria, SSS, SAS, ASA, all require three pieces of information. It is interesting, however, that not all three pieces of information about sides and angles are sufficient to determine a triangle up to congruence. |
| Inscribing a square in a circle: | This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context. |
| Construction of perpendicular bisector: | This problem solving task challenges students to construct a perpendicular bisector of a given segment. |
| Reflected Triangles: | This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected. |
| Right triangles inscribed in circles II: | This problem solving task asks students to explain certain characteristics about a triangle. |
| Locating Warehouse: | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Angle bisection and midpoints of line segments: | This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts. |
| Is This a Rectangle?: | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |
| Name |
Description |
| Bank Shot: | This task asks students to use similarity to solve a problem in a context that will be familiar to many, though most students are accustomed to using intuition rather than geometric reasoning to set up the shot. |
| Extensions, Bisections and Dissections in a Rectangle: | This task involves a reasonably direct application of similar triangles, coupled with a moderately challenging procedure of constructing a diagram from a verbal description. |
| Solar Eclipse: | This problem solving task encourages students to explore why solar eclipses are rare by examining the radius of the sun and the furthest distance between the moon and the earth. |
| Mt. Whitney to Death Valley: | This task engages students in an open-ended modeling task that uses similarity of right triangles. |
| Joining two midpoints of sides of a triangle: | Using a triangle with line through it, students are tasked to show the congruent angles, and conclude if one triangle is similar to the other. |
| Unit Squares and Triangles: | This problem solving task asks students to find the area of a triangle by using unit squares and line segments. |
| When Does SSA Work to Determine Triangle Congruence?: | In this problem, we considered SSA. The triangle congruence criteria, SSS, SAS, ASA, all require three pieces of information. It is interesting, however, that not all three pieces of information about sides and angles are sufficient to determine a triangle up to congruence. |
| Inscribing a square in a circle: | This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context. |
| Construction of perpendicular bisector: | This problem solving task challenges students to construct a perpendicular bisector of a given segment. |
| Reflected Triangles: | This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected. |
| Right triangles inscribed in circles II: | This problem solving task asks students to explain certain characteristics about a triangle. |
| Locating Warehouse: | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Angle bisection and midpoints of line segments: | This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts. |
| Is This a Rectangle?: | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |