Standard #: MA.912.AR.3.6

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.912.AR.1.3
• MA.912.AR.1.7

 

Terms from the K-12 Glossary

• Quadratic Function 
• $x$-intercept 
• $y$-intercept

 

Vertical Alignment

Previous Benchmarks

• MA.8.AR.1.2

Next Benchmarks

• MA.912.AR.6.4
• MA.912.AR.6.5

 

Purpose and Instructional Strategies

In grade 8, students multiplied two linear expressions to obtain a quadratic expression. In Algebra I, students transform a quadratic function to highlight and interpret its vertex or its zeroes. In later courses, students will determine key features of higher degree polynomials. 

• Instruction includes making connections to various forms of quadratic equations to show their equivalency. Students should understand and interpret when one form might be more useful than other depending on the context. 
  • Standard Form
    Can be described by the equation $y$ = $a$$x$²+ $b$$x$ + $c$, where $a$, $b$ and $c$ are any rational number. This form can be useful when identifying the $y$-intercept.  
  • Factored form
    Can be described by the equation $y$ = $a$($x$ − $r$₁)($x$ − $r$₂), where $r$₁ and  $r$₂ are real numbers and the roots, or $x$-intercepts. This form can be useful when identifying the $x$-intercepts, or roots. 
  • Vertex form
    Can be described by the equation $y$ = $a$($x$ − $h$)² + $k$, where the point ($h$, $k$) is the vertex. This form can be useful when identifying the vertex. 
• Instruction includes the use of $x$-$y$ notation and function notation. 
• Most contexts for this benchmark will present functions in standard form. Depending on their perspectives, students might take several approaches to determine vertices and zeros. Have students discuss strategies they might use. Let students know they should use the approach that is most efficient for them (MTR.3.1). 
  • To determine zeros, students could use the quadratic formula or convert the function into factored form, or complete the square, or use Loh’s method. 
• To determine the vertex, students could convert the function into vertex form or determine the axis of symmetry ($x$ = $\frac{\text{<math><mi>−b</mi></math>}}{\text{<math><mi>2a</mi></math>}}$). Calculate this value from one of the previous  functions discussed and guide students to see that the vertex of each parabola falls on the line of symmetry. Considering this, they can substitute that $y$-value into the function to determine the corresponding $y$-value of the vertex.

 

Common Misconceptions or Errors

• Some students may have difficulty interpreting the meaning of the zeros and vertex.

 

Strategies to Support Tiered Instruction

• Teacher provides a graphic organizer for key terms (zeros and vertex) that can be created using information provided in a given problem. 

• Teacher co-creates a graphic organizer to compare real-world and mathematical contexts related to quadratics. 
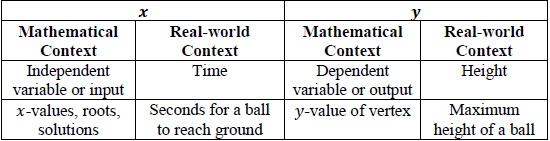
  • For example, the chart below can be used to compare mathematical terms with real-world context. 
    
    
    

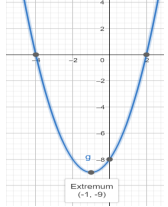
• Teacher provides a visual aid, including using graphing software, to interpret the zeros and vertex of a quadratic function. Students can compare definitions and examples to determine the zeros and vertex of the parabola. 
  • For example, the roots of the graph shown are (2, 0) and (−4, 0). The locations on the graph that intersect the $x$-axis are the roots. The roots are also the solutions of the quadratic. The vertex of the graph shown is (−1, −9). The vertex is the minimum or maximum point (sometimes called the extrema) of the parabola. The vertex is also the point where the quadratic changes from decreasing to increasing or from increasing to decreasing, and is halfway between the roots.

Instructional Tasks

Instructional Task 1 (MTR.3.1, MTR.6.1, MTR.7.1) 

• A diver jumps off a cliff 5 meters high into a lake. The diver’s position can be represented by the function $h$($t$) = −4.9$t$²+ 1.5$t$ + 5, where $h$ represents the diver’s height relative to the lake’s surface and $t$ represents the time in seconds. 
  • Part A. Determine the roots of the function described. 
  • Part B. Interpret each with respect to the situation. 

Instructional Task 2 (MTR.3.1, MTR.7.1) *The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.