Standard #: MA.912.AR.2.8

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

• MA.912.AR.4.1
• MA.912.AR.4.3  
• MA.912.AR.9.1
• MA.912.AR.9.4
• MA.912.AR.9.6

 

Terms from the K-12 Glossary

• Coordinate Plane  
• Linear Expression

 

Vertical Alignment

Previous Benchmarks

• MA.8.AR.3.4

Next Benchmarks

• MA.912.AR.3.10 
• MA.912.AR.9.8

 

Purpose and Instructional Strategies

In grade 8, students graphed linear two-variable equations. In Algebra I, students graph the solution set to a two-variable linear inequality. In later courses, students will solve problems involving linear programming and will graph the solutions sets of two-variable quadratic inequalities. 

• Instruction includes the use of linear inequalities in standard form, slope-intercept form and point-slope form. Include examples in which one variable has a coefficient of zero such as $x$ < −$\frac{\text{17}}{\text{5}}$.
• Instruction includes the connection to graphing solution sets of one-variable inequalities on a number line; recognizing whether the boundary line should be dotted (exclusive) or solid (inclusive). Additionally, have students use a test point to confirm which side of the line should be shaded (MTR.6.1). 
• Students should recognize that the inequality symbol only directs where the line is shaded (above or below) for inequalities when in slope-intercept form. Students shading inequalities in other forms will need to use a test point to determine the correct half-plane to shade.

 

Common Misconceptions or Errors

• Students often choose to shade the wrong half-plane when graphing two-variable linear inequalities. 
• Students may think that the inequality symbol’s orientation always determines the side of the line to shade. 
  • For example, students may say that inequalities with a less than symbol should be shaded below the line while inequalities with a greater than symbol should be shaded above the line. This typically happens after graphing multiple inequalities in slope-intercept form. To address this, provides counterexamples to this such as 3$x$ − 2$y$ < 15 $o$$r$ − 4$x$ − 7 ≥ $y$. Use these counterexamples to emphasize the benefit of using a test point to confirm the direction of shading.

 

Strategies to Support Tiered Instruction

• Instruction includes opportunities to use a highlighter to identify the phrases “is less than,” “is greater than,” “is less than or equal to,” and “is greater than or equal to” when writing inequalities. 
• Teacher provides instruction modeling how to correctly identify the solution set of a linear inequality given in slope-intercept form. After graphing, students can circle the y intercept. If the inequality is in form $y$ < $m$$x$ + $b$ or $y$ ≤ $m$$x$ + $b$, the solution set is the half-plane that contains the $y$-axis values below the $y$-intercept. If the inequality is in form $y$ > $m$$x$ + $b$ or $y$ ≥ $m$$x$ + $b$, the solution set is the half-plane that contains the $y$- axis values above the $y$-intercept. 
• Instruction includes opportunities to graph the boundary line of a system of inequalities, based on an inaccurate translation from word problem. To assist in determining the boundary line for the system, students can create a graphic organizer like the one below. 

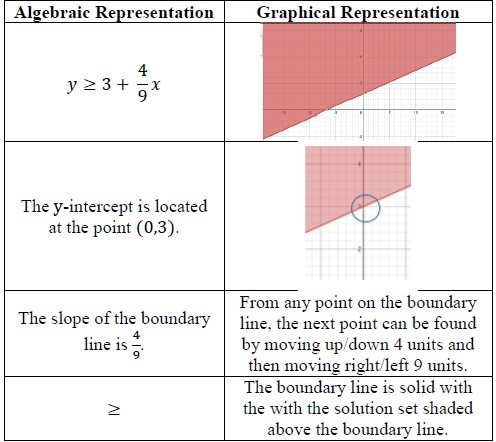
• Instruction includes making the connection between the algebraic and graphical representations of a two-variable linear inequality and its key features. 
  • For example, teacher can provide a graphic organizer such as the one below. 

• Instruction includes opportunities to identify a test point to plug into an inequality. It is usually easiest to use the origin (0,0) as it makes mental calculations easier. If the point selected creates a true statement, their inequality is true and they should shade in the half-plane containing that point. If it creates a false statement, they should shade in the half-plane not containing that point. By using a test point, students avoid the mistake of thinking that the direction of the inequality determines the shading. 
  • For example, the points (−4,3), (0,0), (3,2) and (3, −1) were used to determine where to shade for the inequality 4$x$ − 3$y$ < 6 shown below.

 

Instructional Tasks

Instructional Task 1 (MTR.7.1)  

• Penelope is planning to bake cakes and cookies to sell for an upcoming school fundraiser.  
• Each cake requires 1$\frac{\text{3}}{\text{4}}$ cups of flour and each batch of cookies requires 2$\frac{\text{1}}{\text{4}}$ cups of flour. 
• Penelope bought 3 bags of flour. Each bag contains around 17 cups of flour. 
  • Part A. Assuming she has all the other ingredients needed, create a graph to show all the possible combinations of cakes and batches of cookies Penelope could make. 
  • Part B. Create constraints for this given situation.

 

Instructional Items

Instructional Item 1 

• Graph the solution set to the inequality $y$ + 3 > −2($x$ − 2).

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.