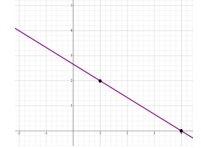
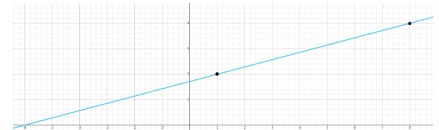
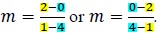Write a linear two-variable equation to represent the relationship between two quantities from a graph, a written description or a table of values within a mathematical or real-world context.
Instruction includes the use of standard form, slope-intercept form and point-slope form, and the conversion between these forms.
| Course Number1111 |
Course Title222 |
| 1200310: | Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200320: | Algebra 1 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200370: | Algebra 1-A (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912080: | Access Algebra 1A (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 1200315: | Algebra 1 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200375: | Algebra 1-A for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912075: | Access Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| Name |
Description |
| What Is the Point? | Students are asked to explain the relationship between a given linear equation and both a point on its graph and a point not on its graph. |
| Finding Solutions | Students are asked to explain the relationship between a given linear equation and both a point on its graph and a point not on its graph. |
| Functions From Graphs | Students are asked to write a function given its graph. |
| Writing a Function From Ordered Pairs | Students are given a table of values and are asked to write a linear function. |
| The Cost of Water | Students are asked to write a function to model the relationship between two variables described in a real-world context. |
| Tee It Up | Students are asked to write an equation in three variables from a verbal description.
Note: This task may assess skills that exceed the general expectation for this mathematical concept at this grade level. The task is intended for students who have demonstrated mastery within the scope of instruction who may be ready for a more rigorous extensions of the content. As with all materials, ensure to gauge the readiness of students or adapt according to students needs prior to administration. |
| Tech Repairs | Students are asked to write an equation in two variables from a verbal description. |
| Name |
Description |
| Home Lines | Students will create an outline of a room and write equations of the lines that contain the sides of the room. This lesson provides an opportunity to review and reinforce writing equations of lines (including horizontal and vertical lines) and to apply the relationship between the slopes of parallel and perpendicular lines. |
| Space Equations | In this lesson, students model the orbit of a satellite and the trajectory of a missile with a system of equations. They solve the equations both graphically and algebraically. |
| What's Slope got to do with it? | Students will interpret the meaning of slope and y-intercept in a wide variety of examples of real-world situations modeled by linear functions. |
| Slippery Slopes | This lesson will not only reinforce students understanding of slope and y-intercept, but will also ensure the students understand how it can be modeled in a real world situation. The focus of this lesson is to emphasize that slope is a rate of change and the y-intercept the value of y when x is zero. Students will be able to read a problem and create a linear equation based upon what they read. They will then make predictions based upon this information. |
| Modeling Situations With Linear Equations | This lesson unit is intended to help you assess how well students use algebra in context, and in particular, how well students:
- Explore relationships between variables in everyday situations.
- Find unknown values from known values.
- Find relationships between pairs of unknowns, and express these as tables and graphs.
- Find general relationships between several variables, and express these in different ways by rearranging formulae.
|
| Solving Linear Equations in Two Variables | This lesson unit is intended to help you assess how well students can formulate and solve problems using algebra and, in particular, to identify and help students who have difficulties solving a problem using two linear equations with two variables and interpreting the meaning of algebraic expressions. |
| Which Function? | This activity has students apply their knowledge to distinguish between numerical data that can be modeled in linear or exponential forms. Students will create mathematical models (graph, equation) that represent the data and compare these models in terms of the information they show and their limitations. Students will use the models to compute additional information to predict future outcomes and make conjectures based on these predictions. |
| Don't Blow the Budget! | Students use systems of equations and inequalities to solve real world budgeting problems involving two variables. |
| Movie Theater MEA | In this Model Eliciting Activity, MEA, students create a plan for a movie theater to stay in business. Data is provided for students to determine the best film to show, and then based on that decision, create a model of ideal sales. Students will create equations and graph them to visually represent the relationships.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Name |
Description |
| What functions do two graph points determine? | This problem solving task challenges students to find the linear, exponential and quadratic functions based on two points. |
| US Population 1982-1988 | This problem solving task asks students to predict and model US population based on a chart of US population data from 1982 to 1988. |
| Taxi! | This simple conceptual problem does not require algebraic manipulation, but requires students to articulate the reasoning behind each statement. Students are asked to verify a given linear equation from data in a table and interpret its key components in context. |
| Sandia Aerial Tram | The task provides an opportunity for students to engage in detailed analysis of the rate of change of the elevation. |
| Do two points always determine a linear function? | In a geometric context, two distinct points ??1 and ??2 always determine a unique line in the Cartesian plane (this is one of the basic postulates of Euclidean geometry). Only the non-vertical lines, however, can be described by the graph of a function ??(??)=????+??. This task focuses on producing an explicit function ??(??) as long as the line is not vertical.
This problem allows the student to think geometrically about lines and then relate this geometry to linear functions. Or the student can work algebraically with equations to find the explicit equation of the line through two points (when that line is not vertical). |
| Cash Box | The given solutions for this task involve the creation and solving of a system of two equations and two unknowns, with the caveat that the context of the problem implies that we are interested only in non-negative integer solutions. Indeed, in the first solution, we must also restrict our attention to the case that one of the variables is further even. This aspect of the task is illustrative of the mathematical practice of modeling with mathematics, and crucial as the system has an integer solution for both situations, that is, whether we include the dollar on the floor in the cash box or not. |
| Two Lines | In this task, we are given the graph of two lines including the coordinates of the intersection point and the coordinates of the two vertical intercepts and are asked for the corresponding equations of the lines. It is a very straightforward task that connects graphs and equations and solutions and intersection points. |
| Selling Fuel Oil at a Loss | The task is a modeling problem which ties in to financial decisions faced routinely by businesses, namely the balance between maintaining inventory and raising short-term capital for investment or re-investment in developing the business. |
| How Many Solutions? | The student is given the equation 5x-2y=3 and asked, if possible, to write a second linear equation creating systems resulting in one, two, infinite, and no solutions. |
| Name |
Description |
| What functions do two graph points determine?: | This problem solving task challenges students to find the linear, exponential and quadratic functions based on two points. |
| US Population 1982-1988: | This problem solving task asks students to predict and model US population based on a chart of US population data from 1982 to 1988. |
| Taxi!: | This simple conceptual problem does not require algebraic manipulation, but requires students to articulate the reasoning behind each statement. Students are asked to verify a given linear equation from data in a table and interpret its key components in context. |
| Sandia Aerial Tram: | The task provides an opportunity for students to engage in detailed analysis of the rate of change of the elevation. |
| Do two points always determine a linear function?: | In a geometric context, two distinct points ??1 and ??2 always determine a unique line in the Cartesian plane (this is one of the basic postulates of Euclidean geometry). Only the non-vertical lines, however, can be described by the graph of a function ??(??)=????+??. This task focuses on producing an explicit function ??(??) as long as the line is not vertical.
This problem allows the student to think geometrically about lines and then relate this geometry to linear functions. Or the student can work algebraically with equations to find the explicit equation of the line through two points (when that line is not vertical). |
| Cash Box: | The given solutions for this task involve the creation and solving of a system of two equations and two unknowns, with the caveat that the context of the problem implies that we are interested only in non-negative integer solutions. Indeed, in the first solution, we must also restrict our attention to the case that one of the variables is further even. This aspect of the task is illustrative of the mathematical practice of modeling with mathematics, and crucial as the system has an integer solution for both situations, that is, whether we include the dollar on the floor in the cash box or not. |
| Two Lines: | In this task, we are given the graph of two lines including the coordinates of the intersection point and the coordinates of the two vertical intercepts and are asked for the corresponding equations of the lines. It is a very straightforward task that connects graphs and equations and solutions and intersection points. |
| Selling Fuel Oil at a Loss: | The task is a modeling problem which ties in to financial decisions faced routinely by businesses, namely the balance between maintaining inventory and raising short-term capital for investment or re-investment in developing the business. |
| How Many Solutions?: | The student is given the equation 5x-2y=3 and asked, if possible, to write a second linear equation creating systems resulting in one, two, infinite, and no solutions. |
| Name |
Description |
| What functions do two graph points determine?: | This problem solving task challenges students to find the linear, exponential and quadratic functions based on two points. |
| US Population 1982-1988: | This problem solving task asks students to predict and model US population based on a chart of US population data from 1982 to 1988. |
| Taxi!: | This simple conceptual problem does not require algebraic manipulation, but requires students to articulate the reasoning behind each statement. Students are asked to verify a given linear equation from data in a table and interpret its key components in context. |
| Sandia Aerial Tram: | The task provides an opportunity for students to engage in detailed analysis of the rate of change of the elevation. |
| Do two points always determine a linear function?: | In a geometric context, two distinct points ??1 and ??2 always determine a unique line in the Cartesian plane (this is one of the basic postulates of Euclidean geometry). Only the non-vertical lines, however, can be described by the graph of a function ??(??)=????+??. This task focuses on producing an explicit function ??(??) as long as the line is not vertical.
This problem allows the student to think geometrically about lines and then relate this geometry to linear functions. Or the student can work algebraically with equations to find the explicit equation of the line through two points (when that line is not vertical). |
| Cash Box: | The given solutions for this task involve the creation and solving of a system of two equations and two unknowns, with the caveat that the context of the problem implies that we are interested only in non-negative integer solutions. Indeed, in the first solution, we must also restrict our attention to the case that one of the variables is further even. This aspect of the task is illustrative of the mathematical practice of modeling with mathematics, and crucial as the system has an integer solution for both situations, that is, whether we include the dollar on the floor in the cash box or not. |
| Two Lines: | In this task, we are given the graph of two lines including the coordinates of the intersection point and the coordinates of the two vertical intercepts and are asked for the corresponding equations of the lines. It is a very straightforward task that connects graphs and equations and solutions and intersection points. |
| Selling Fuel Oil at a Loss: | The task is a modeling problem which ties in to financial decisions faced routinely by businesses, namely the balance between maintaining inventory and raising short-term capital for investment or re-investment in developing the business. |
| How Many Solutions?: | The student is given the equation 5x-2y=3 and asked, if possible, to write a second linear equation creating systems resulting in one, two, infinite, and no solutions. |