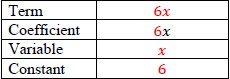
Identify and interpret parts of an equation or expression that represent a quantity in terms of a mathematical or real-world context, including viewing one or more of its parts as a single entity.
to make a prediction about the camel population in Australia. He identifies the growth factor as (1+.1), or 1.1, and states that the camel population will grow at an annual rate of 10% per year.
Parts of an expression include factors, terms, constants, coefficients and variables.
| Course Number1111 |
Course Title222 |
| 1200310: | Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200320: | Algebra 1 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200330: | Algebra 2 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200340: | Algebra 2 Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200370: | Algebra 1-A (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200380: | Algebra 1-B (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912080: | Access Algebra 1A (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912090: | Access Algebra 1B (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 1200315: | Algebra 1 for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200375: | Algebra 1-A for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1200385: | Algebra 1-B for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912075: | Access Algebra 1 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 7912095: | Access Algebra 2 (Specifically in versions: 2016 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current)) |
| 1210305: | Mathematics for College Statistics (Specifically in versions: 2022 - 2024, 2024 and beyond (current)) |
| 1200388: | Mathematics for Data and Financial Literacy Honors (Specifically in versions: 2022 - 2024, 2024 and beyond (current)) |
| 1200384: | Mathematics for Data and Financial Literacy (Specifically in versions: 2022 - 2024, 2024 and beyond (current)) |
| 7912120: | Access Mathematics for Data and Financial Literacy (Specifically in versions: 2022 - 2023, 2023 and beyond (current)) |
| Name |
Description |
| The Laws of Sine and Cosine | In this lesson, students determine when to use the Law of Cosine and/or the Law of Sine to calculate the measures of sides and angles of non-right triangles. |
| Free Fall Clock and Reaction Time! | This will be a lesson designed to introduce students to the concept of 9.81 m/s2 as a sort of clock that can be used for solving all kinematics equations where a = g. |
| Following the Law of Sine | This lesson introduces the law of sine. It is designed to give students practice in using the law to guide understanding. The summative assessment requires students to use the law of sine to plan a city project. |
| My Favorite Slice | The lesson introduces students to sectors of circles and illustrates ways to calculate their areas. The lesson uses pizzas to incorporate a real-world application for the of area of a sector. Students should already know the parts of a circle, how to find the circumference and area of a circle, how to find an arc length, and be familiar with ratios and percentages. |
| Sorting Equations and Identities | This lesson is intended to help you assess how well students are able to:
- Recognize the differences between equations and identities.
- Substitute numbers into algebraic statements in order to test their validity in special cases.
- Resist common errors when manipulating expressions such as 2(x – 3) = 2x – 3; (x + 3)2 = x2 + 32.
- Carry out correct algebraic manipulations.
It also aims to encourage discussion on some common misconceptions about algebra. |
| Modeling Situations With Linear Equations | This lesson unit is intended to help you assess how well students use algebra in context, and in particular, how well students:
- Explore relationships between variables in everyday situations.
- Find unknown values from known values.
- Find relationships between pairs of unknowns, and express these as tables and graphs.
- Find general relationships between several variables, and express these in different ways by rearranging formulae.
|
| Acceleration | In this lesson students will learn to:
- Identify changes in motion that produce acceleration.
- Describe examples of objects moving with constant acceleration.
- Calculate the acceleration of an object, analytically, and graphically.
- Interpret velocity-time graph, and explain the meaning of the slope.
- Classify acceleration as positive, negative, and zero.
- Describe instantaneous acceleration.
|
| Falling for Gravity | Students will investigate the motion of three objects of different masses undergoing free fall. Additionally, students will:
- Use spark timers to collect displacement and time data.
- Use this data to calculate the average velocity for the object during each interval.
- Graph this data on a velocity versus time graph, V-t. They find the slope of this graph to calculate acceleration.
- Calculate the falling object's acceleration from their data table and graph this data on an acceleration versus time graph, a-t.
- Use their Spark timer data paper, cut it into intervals, and paste these intervals into their displacement versus time graph.
|
| How much is your time worth? | This lesson is designed to help students solve real-world problems involving compound and continuously compounded interest. Students will also be required to translate word problems into function models, evaluate functions for inputs in their domains, and interpret outputs in context. |
| Efficient Storage | The topic of this MEA is work and power. Students will be assigned the task of hiring employees to complete a given task. In order to make a decision as to which candidates to hire, the students initially must calculate the required work. The power each potential employee is capable of, the days they are available to work, the percentage of work-shifts they have missed over the past 12 months, and the hourly pay rate each worker commands will be provided to assist in the decision process. Full- and/or part-time positions are available. Through data analysis, the students will need to evaluate which factors are most significant in the hiring process. For instance, some groups may prioritize speed of work, while others prioritize cost or availability/dependability.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Turning Tires Model Eliciting Activity | The Turning Tires MEA provides students with an engineering problem in which they must work as a team to design a procedure to select the best tire material for certain situations. The main focus of the MEA is applying surface area concepts and algebra through modeling. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Name |
Description |
| Quadrupling Leads to Halving | Students explore the structure of the operation s/(vn). This question provides students with an opportunity to see expressions as constructed out of a sequence of operations: first taking the square root of n, then dividing the result of that operation into s. |
| A Saturating Exponential | This task provides an interesting context to ask students to estimate values in an exponential function using a graph. |
| The Physics Professor | Students write explanations of the structure and function of a mathematical expression. |
| Throwing Horseshoes | Students evaluate equivalent constructions of the same expression to determine which is the most useful for determining a maximum value. |
| The Bank Account | Students explore an expression that calculates the balance of a bank account with compounding interest. |
| Radius of a Cylinder | Students are asked to interpret the effect on the value of an expression given a change in value of one of the variables. |
| Mixing Fertilizer | Students examine and answer questions related to a scenario similar to a "mixture" problem involving two different mixtures of fertilizer. In this example, students determine and then compare expressions that correspond to concentrations of various mixtures. Ultimately, students generalize the problem and verify conclusions using algebraic rather than numerical expressions. |
| Mixing Candies | Students are asked to interpret expressions and equations within the context of the amounts of caramels and truffles in a box of candy. |
| Kitchen Floor Tiles | This problem asks students to consider algebraic expressions calculating the number of floor tiles in given patterns. The purpose of this task is to give students practice in reading, analyzing, and constructing algebraic expressions, attending to the relationship between the form of an expression and the context from which it arises. The context here is intentionally thin; the point is not to provide a practical application to kitchen floors, but to give a framework that imbues the expressions with an external meaning. |
| Increasing or Decreasing? Variation 1 | Students examine variable expression that is a complex fraction with two distinct unit fractions in the denominator. Students are asked to consider how increasing one variable will affect the value of the entire expression. The variable expression is used in physics and describes the combined resistance of two resistors in parallel. |
| Delivery Trucks | This resource describes a simple scenario which can be represented by the use of variables. Students are asked to examine several variable expressions, interpret their meaning, and describe what quantities they each represent in the given context. |
| Animal Populations | In this task students interpret the relative size of variable expressions involving two variables in the context of a real world situation. All given expressions can be interpreted as quantities that one might study when looking at two animal populations. |
| Name |
Description |
| Quadrupling Leads to Halving: | Students explore the structure of the operation s/(vn). This question provides students with an opportunity to see expressions as constructed out of a sequence of operations: first taking the square root of n, then dividing the result of that operation into s. |
| A Saturating Exponential: | This task provides an interesting context to ask students to estimate values in an exponential function using a graph. |
| Radius of a Cylinder: | Students are asked to interpret the effect on the value of an expression given a change in value of one of the variables. |
| Mixing Fertilizer: | Students examine and answer questions related to a scenario similar to a "mixture" problem involving two different mixtures of fertilizer. In this example, students determine and then compare expressions that correspond to concentrations of various mixtures. Ultimately, students generalize the problem and verify conclusions using algebraic rather than numerical expressions. |
| Mixing Candies: | Students are asked to interpret expressions and equations within the context of the amounts of caramels and truffles in a box of candy. |
| Kitchen Floor Tiles: | This problem asks students to consider algebraic expressions calculating the number of floor tiles in given patterns. The purpose of this task is to give students practice in reading, analyzing, and constructing algebraic expressions, attending to the relationship between the form of an expression and the context from which it arises. The context here is intentionally thin; the point is not to provide a practical application to kitchen floors, but to give a framework that imbues the expressions with an external meaning. |
| Delivery Trucks: | This resource describes a simple scenario which can be represented by the use of variables. Students are asked to examine several variable expressions, interpret their meaning, and describe what quantities they each represent in the given context. |
| Animal Populations: | In this task students interpret the relative size of variable expressions involving two variables in the context of a real world situation. All given expressions can be interpreted as quantities that one might study when looking at two animal populations. |
| Name |
Description |
| Quadrupling Leads to Halving: | Students explore the structure of the operation s/(vn). This question provides students with an opportunity to see expressions as constructed out of a sequence of operations: first taking the square root of n, then dividing the result of that operation into s. |
| A Saturating Exponential: | This task provides an interesting context to ask students to estimate values in an exponential function using a graph. |
| Radius of a Cylinder: | Students are asked to interpret the effect on the value of an expression given a change in value of one of the variables. |
| Mixing Fertilizer: | Students examine and answer questions related to a scenario similar to a "mixture" problem involving two different mixtures of fertilizer. In this example, students determine and then compare expressions that correspond to concentrations of various mixtures. Ultimately, students generalize the problem and verify conclusions using algebraic rather than numerical expressions. |
| Mixing Candies: | Students are asked to interpret expressions and equations within the context of the amounts of caramels and truffles in a box of candy. |
| Kitchen Floor Tiles: | This problem asks students to consider algebraic expressions calculating the number of floor tiles in given patterns. The purpose of this task is to give students practice in reading, analyzing, and constructing algebraic expressions, attending to the relationship between the form of an expression and the context from which it arises. The context here is intentionally thin; the point is not to provide a practical application to kitchen floors, but to give a framework that imbues the expressions with an external meaning. |
| Delivery Trucks: | This resource describes a simple scenario which can be represented by the use of variables. Students are asked to examine several variable expressions, interpret their meaning, and describe what quantities they each represent in the given context. |
| Animal Populations: | In this task students interpret the relative size of variable expressions involving two variables in the context of a real world situation. All given expressions can be interpreted as quantities that one might study when looking at two animal populations. |
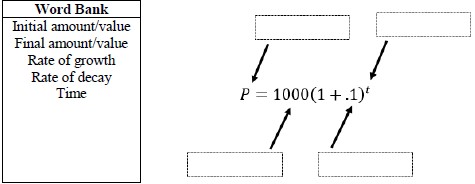


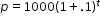 to make a prediction about the camel population in Australia. He identifies the growth factor as (1+.1), or 1.1, and states that the camel population will grow at an annual rate of 10% per year.
to make a prediction about the camel population in Australia. He identifies the growth factor as (1+.1), or 1.1, and states that the camel population will grow at an annual rate of 10% per year.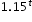 can be rewritten as
can be rewritten as 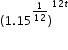 which is approximately equivalent to
which is approximately equivalent to 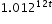 . This latter expression reveals the approximate equivalent monthly interest rate of 1.2% if the annual rate is 15%.
. This latter expression reveals the approximate equivalent monthly interest rate of 1.2% if the annual rate is 15%.