Standard #: MA.8.GR.2.3


This document was generated on CPALMS - www.cpalms.org



Describe and apply the effect of a single transformation on two-dimensional figures using coordinates and the coordinate plane.


Clarifications


Clarification 1: Within this benchmark, transformations are limited to reflections, translations, rotations or dilations of images. 
Clarification 2: Lines of reflection are limited to the x-axis, y-axis or lines parallel to the axes.

Clarification 3: Rotations must be about the origin and are limited to 90°, 180°, 270° or 360°.

Clarification 4: Dilations must be centered at the origin.



General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 8
Strand: Geometric Reasoning
Standard: Understand similarity and congruence using models and transformations.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

  • NA
 

Terms from the K-12 Glossary

  • Coordinates
  • Coordinate Plane

 

Vertical Alignment

Previous Benchmarks

Next Benchmarks

 

Purpose and Instructional Strategies

In grade 6, students plotted rational-number ordered pairs in all four quadrants as well as identified the x- or y-axis as a line of reflection when two ordered pairs have an opposite x- or y-coordinate. In grade 7, students solved mathematical and real-world problems involving scale factors. In grade 8, students apply a single transformation using coordinates and the coordinate plane. In Algebra 1, students will apply a single transformation to functions. In Geometry, students will describe transformations given a preimage and an image and represent the transformation algebraically using coordinates and use them to study congruence and similarity.
  • Use grid paper to illustrate translations of a line or triangle to demonstrate the relationship between them and a new image. Then, illustrate translations of more complex figures such as polygons.
  • Transformations can be noted using the prime notation (′) for the image and its vertices. The preimage and its vertices will not have prime notation.
    • For example, the picture below showcases a single transformation.
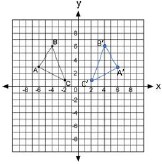
      single transformation.
  • Problem types include telling which direction, clockwise or counterclockwise, for rotations.
  • Instruction includes looking for patterns to create rules for transformations on the coordinate plane.
  • For mastery of this benchmark, single transformations include one vertical translation or one horizontal translation. A vertical and horizontal translation would be considered two transformations.

 

Common Misconceptions or Errors

  • Students may incorrectly visualize transformation on the coordinate plane. To address this misconception, provide students with manipulatives.
  • Students may incorrectly apply rules for transformations. To address this misconception, students should generate examples and non-examples of given transformations.

 

Strategies to Support Tiered Instruction

  • Teacher supports understanding of transformations on the coordinate place by providing examples using geometric software. Instruction includes the use of manipulatives and graph paper.
  • Teacher reminds students when plotting points on a coordinate plane that they can first find the x-coordinate on the x-axis (horizontal axis) and then find the y-coordinate on the y-axis (vertical axis).
  • Teacher reviews vocabulary discussing the meaning of the terms.
    • Translation is a vertical or horizontal slide of the figure. To determine the coordinates of the image of a translated figure you must add or subtract the horizontal distance to the x-coordinate of each vertex and add or subtract the vertical distance to the y-coordinate of each vertex. (Note that in later courses, students learn that translation can also occur diagonally.)
    • Preimage is the figure before any transformations are performed.
    • Image is the figure after a transformation is performed.
  • Teacher co-creates a graphic organizer to generate examples and non-examples of reflections, translations, rotations, or dilations of images.
  • Teacher provides instruction to support understanding of applying the translation to all vertices, not just one vertex.
  • Teacher reviews directions of rotations. Clockwise is the direction the hands go on an analog clock Clockwise direction. Counterclockwise is the opposite direction of the hands on an analog clock Counterclockwise direction.
    • For example, which quadrant would the image be in if you rotated the figure?
      • 90 degrees clockwise
      • 90 degrees counterclockwise
      • 180 degrees clockwise
      • 180 degrees counterclockwise
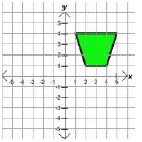
        Image in a Quadrant
  • Teacher reviews which is the x-axis and which is the y-axis for students that incorrectly reflect across the wrong axis. Teacher co-creates anchor chart explaining different parts of coordinate plane, and how to plot and label points.
    • For example, teachers could ask students which quadrant the image would be in if you reflected the figure across the x-axis or across the y-axis.
  • Instruction includes providing students with manipulatives for students that incorrectly visualize transformations on the coordinate plane.

 

Instructional Tasks

Instructional Task 1 (MTR.1.1, MTR.2.1)
Use the information you have learned about transformations to complete the task below.
  • Part A. Using graph paper, plot the following points to create an image on the coordinate plane.
    A(−3,2), B(0,1), C(−3, −1) and D(−1, −1)
  • Part B. Using a different color for each transformation, complete each of the following transformations on the same coordinate plane.
    a. A reflection over the y-axis
    b. A rotation of 180° about the origin
  • Part C. Will any of the new images include the origin?

 

Instructional Items

Instructional Item 1
Find the coordinates of the vertices of the image of triangle IJK after the translation 3 units to the left.
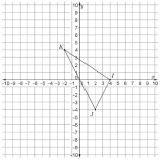
Triangle on a graph

Instructional Item 2
Find the coordinates of the vertices of the image of triangle CAT after a 270° counterclockwise rotation about the origin.
Triangle on a graph

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.


Related Courses

Course Number1111 Course Title222
1205050: M/J Accelerated Mathematics Grade 7 (Specifically in versions: 2014 - 2015, 2015 - 2020, 2020 - 2022, 2022 and beyond (current))
1205070: M/J Grade 8 Pre-Algebra (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1204000: M/J Foundational Skills in Mathematics 6-8 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7812030: Access M/J Grade 8 Pre-Algebra (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.8.GR.2.AP.3 Identify the coordinates of the vertices of a common polygon after a single translation, rotation or dilation on the coordinate plane.


Related Resources

Formative Assessments

Name Description
Translation Coordinates

Students are asked to translate two-dimensional figures in the coordinate plane and identify the coordinates of the vertices of the images.

Rotation Coordinates

Students are asked to rotate two-dimensional figures in the coordinate plane and identify the coordinates of the vertices of the images.

Reflection Coordinates

Students are asked to reflect two-dimensional figures in the coordinate plane and identify the coordinates of the vertices of the images.

Dilation Coordinates

Students are asked to dilate two-dimensional figures in the coordinate plane and identify the coordinates of the vertices of the images.

Lesson Plans

Name Description
Transformations in the Coordinate Plane

In this exploration activity of reflections, translations, and rotations, students are guided to discover general algebraic rules for special classes of transformations in the coordinate plane. This lesson is intended to be used after the development of formal definitions of rotations, translations, and reflections.

"Triangle Congruence Show" Starring Rigid Transformations

Students will be introduced to the definition of congruence in terms of rigid motion and use it to determine if two triangles are congruent.

Reflecting on the Commute

Students are given a set of coordinates that indicate a specific triangle on a coordinate plane. They will also be given a set of three reflections to move the triangle through. Students will then perform three other sequences of reflections to determine if the triangle ends up where it started.

Transformation and Similarity

Using non-rigid motions (dilations), students learn how to show that two polygons are similar. Students will write coordinate proofs confirming that two figures are similar.

Sequence of Transformations

This lesson will assist students in performing multi-step transformations. Students will follow a sequence of transformations on geometric figures using translations, reflections, and rotations.

Regular Polygon Transformation Investigation

This is an introductory lesson on regular polygon transformation for congruency using a hands-on approach.

Construction of Inscribed Regular Hexagon

A GeoGebra lesson for students to become familiar with computer based construction tools. Students work together to construct a regular hexagon inscribed in a circle using rotations. Directions for both a beginner and advanced approach are provided.

Match That!

Students will prove that two figures are congruent based on a rigid motion(s) and then identify the corresponding parts using paragraph proof and vice versa, prove that two figures are congruent based on corresponding parts and then identify which rigid motion(s) map the images.

Isometries with GeoGebra

In this lesson, students explore transformations with GeoGebra and then apply concepts using a straightedge on paper. Students apply rules for each isometry. There is a teacher-driven opening followed by individual student activity.

How Did It Get There? A Series of Transformation Events

Students will perform a series of transformations in order to determine how the pre-image will map onto the final image of a given figure. Students will use patty paper to manipulate their pre-image onto the image. Students will also work in collaborative groups to discuss their findings and will have the opportunity to share their series of transformations with the class. The class discussion will be used to demonstrate that there are several ways for the students to map their pre-image onto the final image.

Dancing For Joy

We have danced our way through reflections, rotations, and translations; now we are ready to take it up a notch by performing a sequence of transformations. Students will also discover the results when reflecting over parallel lines versus intersecting lines.

Turning to Congruence

This lesson uses rigid motions to prove the ASA and HL triangle congruence theorems.

Product of Two Transformations

Students will identify a sequence of steps that will translate a pre-image to its image. Students will also demonstrate that the sequence of two transformations is not always commutative.

How to Land Your Spaceship

Teach your students to maneuver a "spaceship" through a sequence of transformations that will successfully carry it onto its landing pad. GeoGebra directons are provided.

Where Will I Land?

This is a beginning level lesson on predicting the effect of a series of reflections or a quick review of reflections for high school students.

Exploring Congruence Using Transformations

This is an exploratory lesson that elicits the relationship between the corresponding sides and corresponding angles of two congruent triangles.

How do your Air Jordans move?

In this inquiry lesson, students are moving their individually designed Air Jordans around the room to explore rigid transformations on their shoes. They will Predict-Observe-Explain the transformations and then have to explain their successes/failures to other students.

Discovering Dilations

This resource is designed to allow students to discover the effects of dilations on geometric objects using the free online tools in GeoGebra.

Reflections Hands On

Students will use a protractor/ruler to construct reflections and a composite of reflections. They will create transformations using paper cut-outs and a coordinate plane. For independent practice, students will predict and verify sequences of transformations. The teacher will need an LCD Projector and document camera.

Flipping Fours

Students will translate, rotate and reflect quadrilaterals (Parallelogram, Rectangle, Square, Kite, Trapezoid, and Rhombus) using a coordinate grid created on the classroom floor and on graph paper. This activity should be used following guided lessons on transformations.

Let's Reflect On This...

Students will use parallel and intersecting lines on the coordinate plane to transform reflections into translations and rotations.

Dilation Transformation

Students identify dilations, verify that polygons are similar, and use the dilation rule to map dilations. Task cards are provided for independent practice. The PowerPoint also includes detailed illustrations for constructing a dilation using a compass and a straight edge.

Fundamental Property of Reflections

This lesson helps students discover that in a reflection, the line of reflection is the perpendicular bisector of any segment connecting any pre-image point with its reflected image.

Transformers 3

Students will learn the vocabulary of three rigid transformations, reflection, translation, and rotation, and how they relate to congruence. Students will practice transforming figures by applying each isometry and identifying which transformation was used on a figure. The teacher will assign students to take pictures of the three transformations found in the real world.

Rotation of Polygons about a Point

Students will rotate polygons of various shapes about a point. Degrees of rotation vary but generally increase in increments of 90 degrees. Points of rotation include points on the figure, the origin, and points on the coordinate plane. The concept of isometry is addressed.

Transform through the Maze

In this fun activity, students will use rigid transformations to move a triangle through a maze. The activity provides applications for both honors and standard levels. It requires students to perform rotations, translations, and reflections.

Slide to the Left... Slide to the Right!

Students will identify, review, and analyze transformations. They will demonstrate their understanding of transformations in the coordinate plane by creating original graphs of polygons and the images that result from specific transformations.

Problem-Solving Tasks

Name Description
Congruent Triangles

This task has two goals: first to develop student understanding of rigid motions in the context of demonstrating congruence. Secondly, student knowledge of reflections is refined by considering the notion of orientation in part (b). Each time the plane is reflected about a line, this reverses the notions of ''clockwise'' and ''counterclockwise.''

Reflecting Reflections

In this resource, students experiment with the reflection of a triangle in a coordinate plane.

Point Reflection

The purpose of this task is for students to apply a reflection to a single point. The standard asks students to apply the effect of a single transformation on two-dimensional figures. Although this problem only applies a reflection to a single point, it has high cognitive demand if the students are prompted to supply a picture. This is because the coordinates of the point (1000,2012) are very large. If students try to plot this point and the line of reflection on the usual x-y coordinate grid, then either the graph will be too big or else the point will lie so close to the line of reflection that it is not clear whether or not it lies on this line. A good picture requires a careful choice of the appropriate region in the plane and the corresponding labels. Moreover, reflections of two-dimensional figures are found by reflecting individual points.

Reflecting a Rectangle Over a Diagonal

The task is intended for instructional purposes and assumes that students know the properties of rigid transformations. Note that the vertices of the rectangles in question do not fall exactly at intersections of the horizontal and vertical lines on the grid. This means that students need to approximate and this provides an extra challenge. Also providing a challenge is the fact that the grids have been drawn so that they are aligned with the diagonal of the rectangles rather than being aligned with the vertical and horizontal directions of the page. However, this choice of grid also makes it easier to reason about the reflections.

Triangle congruence with coordinates

In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking.

Student Resources

Problem-Solving Tasks

Name Description
Congruent Triangles:

This task has two goals: first to develop student understanding of rigid motions in the context of demonstrating congruence. Secondly, student knowledge of reflections is refined by considering the notion of orientation in part (b). Each time the plane is reflected about a line, this reverses the notions of ''clockwise'' and ''counterclockwise.''

Reflecting Reflections:

In this resource, students experiment with the reflection of a triangle in a coordinate plane.

Point Reflection:

The purpose of this task is for students to apply a reflection to a single point. The standard asks students to apply the effect of a single transformation on two-dimensional figures. Although this problem only applies a reflection to a single point, it has high cognitive demand if the students are prompted to supply a picture. This is because the coordinates of the point (1000,2012) are very large. If students try to plot this point and the line of reflection on the usual x-y coordinate grid, then either the graph will be too big or else the point will lie so close to the line of reflection that it is not clear whether or not it lies on this line. A good picture requires a careful choice of the appropriate region in the plane and the corresponding labels. Moreover, reflections of two-dimensional figures are found by reflecting individual points.

Reflecting a Rectangle Over a Diagonal:

The task is intended for instructional purposes and assumes that students know the properties of rigid transformations. Note that the vertices of the rectangles in question do not fall exactly at intersections of the horizontal and vertical lines on the grid. This means that students need to approximate and this provides an extra challenge. Also providing a challenge is the fact that the grids have been drawn so that they are aligned with the diagonal of the rectangles rather than being aligned with the vertical and horizontal directions of the page. However, this choice of grid also makes it easier to reason about the reflections.

Triangle congruence with coordinates:

In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking.



Parent Resources

Problem-Solving Tasks

Name Description
Congruent Triangles:

This task has two goals: first to develop student understanding of rigid motions in the context of demonstrating congruence. Secondly, student knowledge of reflections is refined by considering the notion of orientation in part (b). Each time the plane is reflected about a line, this reverses the notions of ''clockwise'' and ''counterclockwise.''

Reflecting Reflections:

In this resource, students experiment with the reflection of a triangle in a coordinate plane.

Point Reflection:

The purpose of this task is for students to apply a reflection to a single point. The standard asks students to apply the effect of a single transformation on two-dimensional figures. Although this problem only applies a reflection to a single point, it has high cognitive demand if the students are prompted to supply a picture. This is because the coordinates of the point (1000,2012) are very large. If students try to plot this point and the line of reflection on the usual x-y coordinate grid, then either the graph will be too big or else the point will lie so close to the line of reflection that it is not clear whether or not it lies on this line. A good picture requires a careful choice of the appropriate region in the plane and the corresponding labels. Moreover, reflections of two-dimensional figures are found by reflecting individual points.

Reflecting a Rectangle Over a Diagonal:

The task is intended for instructional purposes and assumes that students know the properties of rigid transformations. Note that the vertices of the rectangles in question do not fall exactly at intersections of the horizontal and vertical lines on the grid. This means that students need to approximate and this provides an extra challenge. Also providing a challenge is the fact that the grids have been drawn so that they are aligned with the diagonal of the rectangles rather than being aligned with the vertical and horizontal directions of the page. However, this choice of grid also makes it easier to reason about the reflections.

Triangle congruence with coordinates:

In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking.



Printed On:4/18/2024 11:15:52 PM
Print Page | Close this window