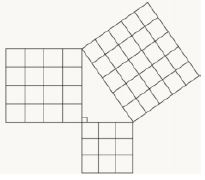
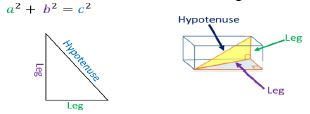
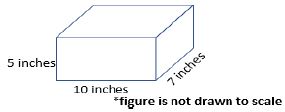
Apply the Pythagorean Theorem to solve mathematical and real-world problems involving unknown side lengths in right triangles.
Instruction includes exploring right triangles with natural-number side lengths to illustrate the Pythagorean Theorem.
| Name |
Description |
| Discovering and Using the Pythagorean Theorem | Students will complete a hands-on activity to discover a geometric proof of the Pythagorean Theorem, and they will use and apply the Pythagorean Theorem to solve examples and real-world situations. |
| Discovering and Using the Pythagorean Theorem | Students will complete a hands-on activity to discover a geometric proof of the Pythagorean Theorem, and they will use and apply the Pythagorean Theorem to solve examples and real-world situations. |
| A Hypotenuse is a WHAT???? | Students are guided through a short history of Pythagoras and a discovery of the Pythagorean Theorem using the squaring of the sides of a right triangle. |
| Discovering and Using the Pythagorean Theorem | Students will complete a hands-on activity to discover a geometric proof of the Pythagorean Theorem, and they will use and apply the Pythagorean Theorem to solve examples and real-world situations. |
| Deriving and Applying the Law of Sines | Students will be introduced to a derivation of the Law of Sines and apply the Law of Sines to solve triangles. |
| Pythagorean Perspective | This lesson serves as an introductory lesson on the Pythagorean Theorem and its converse. It has a hands-on discovery component. This lesson includes worksheets that are practical for individual or cooperative learning strategies. The worksheets contain prior knowledge exercises, practice exercises and a summative assignment. |
| Airplanes in Radar's Range | For a given circle m and point A in a coordinate plane, students will be able to show whether this given point A lies on the circumference of the given circle m using the Pythagorean Theorem. Subsequently, this can be used to prove that an airplane lies within or outside the radar's range with a given radius of detection. |
| How Do You Measure the Immeasurable? | Students will use similar triangles to determine inaccessible measurements. Examples include exploring dangerous caves and discovering craters on Mars. |
| What's the Point? | Students will algebraically find the missing coordinates to create a specified quadrilateral using theorems that represent them, and then algebraically prove their coordinates are correct.
Note: This is not an introductory lesson for this standard. |
| Let's Prove the Pythagorean Theorem | Students will use Triangle Similarity to derive the proof of the Pythagorean Theorem and apply this method to develop the idea of the geometric mean with respect to the relationships in right triangles. |
| Proofs of the Pythagorean Theorem | This lesson enriches the students' perspective of geometric proofs that are not in two-column form. Students will apply algebaic skills and geometric properties to prove the Pythagorean Theorem in a variety of ways. This unit is designed to help you identify and assist students who have difficulties in:
- Interpreting diagrams.
- Identifying mathematical knowledge relevant to an argument.
- Linking visual and algebraic representations.
- Producing and evaluating mathematical arguments.
|
| As the Crow Flies | This two-day lesson teaches students to use the Pythagorean Theorem with simple right triangles on the first day, then progresses to using the theorem to find the distance between two points on a coordinate graph. |
| Origami Boats - Pythagorean Theorem in the Real-World Part 2 | Students will create origami boats and use them to make a net drawing. The drawing will be labeled with measurements, based on the number of squares on the graph for units, such that the students will use the Pythagorean Theorem to find several of the lengths. This is part 2 of a lesson plan for the Pythagorean Theorem. The resource, Applying the Pythagorean Theorem Part 1, with ID #48973, lays the groundwork for this exercise. |
| Just Plane Ol' Area! | Students will construct various figures on coordinate planes and calculate the perimeter and area. Use of the Pythagorean theorem will be required. |
| Applying the Pythagorean Theorem, Part 1 | This lesson applies the Pythagorean Theorem and teaches the foundations of the Pythagorean Theorem. It is part 1 of 2 lessons. The second lesson, Origami Boats - Pythagorean Theorem in the real world, Resource ID 49055, provides an application to use the Pythagorean Theorem for distance in the coordinate plane. |
| Pythagoras - You Clever Dog | This lesson starts with an introduction of the Pythagorean Theorem. It introduces vocabulary, formulas and concepts related to right triangles and the use of the Pythagorean Theorem in the real world. Students will learn the basics through real world application. |
| Alas, Poor Pythagoras, I Knew You Well! #2 | Using different activities, students will find real life uses for the Pythagorean Theorem. |
| A Hypotenuse is a WHAT???? | Students are guided through a short history of Pythagoras and a discovery of the Pythagorean Theorem using the squaring of the sides of a right triangle. |
| Name |
Description |
| The Shortest Line Segment from Point P to Line L | This is a foundational geometry task designed to provide a route for students to develop some fundamental geometric properties that may seem rather obvious at first glance. In this case, the fundamental property in question is that the shortest path from a point to a line meets the line at a right angle which is crucial for many further developments in the subject. |
| Glasses | In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem. |
| A Rectangle in the Coordinate Plane | This task provides an opportunity to apply the Pythagorean theorem to multiple triangles in order to determine the length of the hypotenuse; the converse of the Pythagorean theorem is also required in order to conclude that certain angles are right angles. |
| Bird and Dog Race | The purpose of this task is for students to use the Pythagorean Theorem as a problem-solving tool to calculate the distance between two points on a grid. In this case the grid is also a map, and the street names can be viewed as defining a coordinate system (although the coordinate system is not needed to solve the problem). |
| Is This a Rectangle? | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |
| Area of a Trapezoid | The purpose of this task is for students to use the Pythagorean Theorem to find the unknown side-lengths of a trapezoid in order to determine the area. This problem will require creativity and persistence as students must decompose the given trapezoid into other polygons in order to find its area. |
| Applying the Pythagorean Theorem in a Mathematical Context | Three right triangles surround a shaded triangle; together they form a rectangle measuring 12 units by 14 units. The figure used shows some of the dimensions but is not drawn to scale. Apply the Pythagorean Theorem to prove whether the figure is a right triangle. |
| Areas of Geometric Shapes with the Same Perimeter | This problem is part of a very rich tradition of problems looking to maximize the area enclosed by a shape with fixed perimeter. Only three shapes are considered here because the problem is difficult for more irregular shapes. For example, of all triangles, the one with fixed perimeter P and largest area is the equilateral triangle whose side lengths are all P3 but this is difficult to show because it is not easy to find the area of triangle in terms of the three side lengths (though Heron's formula accomplishes this). Nor is it simple to compare the area of two triangles with equal perimeter without knowing their individual areas. For quadrilaterals, a similar problem arises: showing that of all rectangles with perimeter P the one with the largest area is the square whose side lengths are P4 is a good problem which students should think about. But comparing a square to an irregularly shaped quadrilateral of equal perimeter will be difficult. |
| Running on the Football Field | Students need to reason as to how they can use the Pythagorean Theorem to find the distances ran by Ben Watson and Champ Bailey. The focus here should not be on who ran a greater distance but on seeing how to set up right triangles to apply the Pythagorean Theorem to this problem. Students must use their measurement skills and make reasonable estimates to set up triangles and correctly apply the Theorem. |
| Name |
Description |
| The Shortest Line Segment from Point P to Line L: | This is a foundational geometry task designed to provide a route for students to develop some fundamental geometric properties that may seem rather obvious at first glance. In this case, the fundamental property in question is that the shortest path from a point to a line meets the line at a right angle which is crucial for many further developments in the subject. |
| Glasses: | In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem. |
| A Rectangle in the Coordinate Plane: | This task provides an opportunity to apply the Pythagorean theorem to multiple triangles in order to determine the length of the hypotenuse; the converse of the Pythagorean theorem is also required in order to conclude that certain angles are right angles. |
| Is This a Rectangle?: | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |
| Running on the Football Field: | Students need to reason as to how they can use the Pythagorean Theorem to find the distances ran by Ben Watson and Champ Bailey. The focus here should not be on who ran a greater distance but on seeing how to set up right triangles to apply the Pythagorean Theorem to this problem. Students must use their measurement skills and make reasonable estimates to set up triangles and correctly apply the Theorem. |
| Name |
Description |
| The Shortest Line Segment from Point P to Line L: | This is a foundational geometry task designed to provide a route for students to develop some fundamental geometric properties that may seem rather obvious at first glance. In this case, the fundamental property in question is that the shortest path from a point to a line meets the line at a right angle which is crucial for many further developments in the subject. |
| Glasses: | In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem. |
| A Rectangle in the Coordinate Plane: | This task provides an opportunity to apply the Pythagorean theorem to multiple triangles in order to determine the length of the hypotenuse; the converse of the Pythagorean theorem is also required in order to conclude that certain angles are right angles. |
| Bird and Dog Race: | The purpose of this task is for students to use the Pythagorean Theorem as a problem-solving tool to calculate the distance between two points on a grid. In this case the grid is also a map, and the street names can be viewed as defining a coordinate system (although the coordinate system is not needed to solve the problem). |
| Is This a Rectangle?: | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |
| Area of a Trapezoid: | The purpose of this task is for students to use the Pythagorean Theorem to find the unknown side-lengths of a trapezoid in order to determine the area. This problem will require creativity and persistence as students must decompose the given trapezoid into other polygons in order to find its area. |
| Applying the Pythagorean Theorem in a Mathematical Context: | Three right triangles surround a shaded triangle; together they form a rectangle measuring 12 units by 14 units. The figure used shows some of the dimensions but is not drawn to scale. Apply the Pythagorean Theorem to prove whether the figure is a right triangle. |
| Areas of Geometric Shapes with the Same Perimeter: | This problem is part of a very rich tradition of problems looking to maximize the area enclosed by a shape with fixed perimeter. Only three shapes are considered here because the problem is difficult for more irregular shapes. For example, of all triangles, the one with fixed perimeter P and largest area is the equilateral triangle whose side lengths are all P3 but this is difficult to show because it is not easy to find the area of triangle in terms of the three side lengths (though Heron's formula accomplishes this). Nor is it simple to compare the area of two triangles with equal perimeter without knowing their individual areas. For quadrilaterals, a similar problem arises: showing that of all rectangles with perimeter P the one with the largest area is the square whose side lengths are P4 is a good problem which students should think about. But comparing a square to an irregularly shaped quadrilateral of equal perimeter will be difficult. |
| Running on the Football Field: | Students need to reason as to how they can use the Pythagorean Theorem to find the distances ran by Ben Watson and Champ Bailey. The focus here should not be on who ran a greater distance but on seeing how to set up right triangles to apply the Pythagorean Theorem to this problem. Students must use their measurement skills and make reasonable estimates to set up triangles and correctly apply the Theorem. |